Численные методы решения обыкновенных дифференциальных уравнений и систем: Методические указания к курсовой работе, страница 15

                   

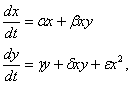
где 

Значения ранее рассмотренных параметров и  начальные условия взять из примера методических указаний. Положить e=0.001. Исследовать поведение на различных временных отрезках.

9.  Решить систему при различных начальных условиях

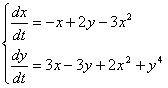
на отрезке [0,2 ] с шагом интегрирования 0.2

Начальные условия

1)      2)   3)   4)

10.  Решить систему при различных начальных условиях

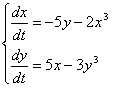
на отрезке [0,3 ] с шагом интегрирования 0.2

Начальные условия

1)      2)   3)   4)

11.  Решить систему при различных начальных условиях

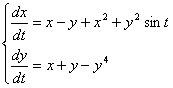
на отрезке [0,3 ] с шагом интегрирования 0.2

Начальные условия

1)      2)   3)   4)

12.   

Рекомендуемая литература.

Основная:

1.  Е. А. Волков. Численные методы. Москва, ”Наука”, 1987.

2.  Л. И. Турчак. Основы численных методов, Москва, ”Наука”, 1987.

3.  Дж. Ортега, У. Пул. Введение в численные методы решения дифференциальных уравнений, Москва, ”Наука”, 1986.

4.  Н. С. Пискунов. Дифференциальное и интегральное исчисление.

5.  Лабораторные работы по курсу “Вычислительная математика и применение ЭВМ”, методическое пособие, Ленинград, 1987.

6.  Г. Н. Воробьева, А. Н. Данилова. Практикум по вычислительной математике, Москва, ”Высшая школа”, 1990.

7.  Турбо Паскаль 7.0. Киев, Торгово-издательское бюро BHV, 1996.

Дополнительная:

1.  Д. Андерсен, Дж. Таннехилл, Р. Плетчер. Вычислительная гидромеханика и теплообмен, М., “Мир”, 1990.

2.  А.Н. Тихонов, Д.Е. Костомаров. Вводные лекции по прикладной математике. М., “Наука”, 1984.