Численные методы решения обыкновенных дифференциальных уравнений и систем: Методические указания к курсовой работе, страница 4

1.3. Метод Рунге-Кутта для решения обыкновенного дифференциального уравнения первого порядка

Далее перейдем к методу Рунге-Кутта, который является, вообще говоря, более точным и имеет практическое значение. Идея метода такая же, как и в методе Эйлера. Приращение функции приближенно выражается в виде линейной комбинации дифференциалов, вычисленных в текущем узле и в окрестных точках узла.

Например, метод Рунге-Кутта второго порядка состоит в последовательном вычислении по формулам:

,                         ,                    (1.5)

x_i+1=x_i+h

где  

Метод Рунге-Кутта третьего порядка состоит в последовательном вычислении по формулам:

,                                (1.6)

x_i+1=x_i+h

где

                                     (1.7)

Метод Рунге-Кутта четвертого  порядка состоит в последовательном вычислении по формулам:

,                                (1.8)

x_i+1=x_i+h

где

                                             (1.9)

Вычисление xi+1 подготавливает значение аргумента для следующего шага и одновременно является текущим для вычисленного значения функции. Таким образом , на каждом шаге можно получить табличные значения xi+1, yi+1  через ранее вычисленные значения x1, yi .   Погрешность вычислений является величиной порядка , или, как говорят, метод дает точность до четвертого порядка (имеет четвертый порядок точности).

1.4. Метод Рунге-Кутта для системы двух обыкновенных дифференциальных уравнений первого порядка.

Аналогично решается задача Коши для системы обыкновенных дифференциальных уравнений первого порядка. Рассмотрим систему  2  уравнений. 1-го порядка

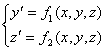                                                                (1.10)

на отрезке [a, b] с начальными условиями

,                                                         (1.11)

Напишем формулы метода Рунге – Кутта вначале  для системы двух уравнений:

                                      (1.12)

                                              xi+1= xi+h

где

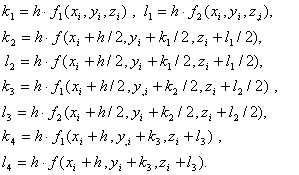                                     (1.13)

Последовательно вычисляются на каждом шаге   , а затем . Во всех вариантах метода   .

1.5. Метод Рунге-Кутта для обыкновенного дифференциального уравнения второго порядка

Рассмотрим уравнение второго порядка, разрешенное относительно второй производной:

                                                   (1.14)

на отрезке [a, b]  с начальными условиями.

Это уравнение легко свести к системе уравнений первого порядка с помощью замены переменных:     . Тогда    и уравнение (1.14) сводится к системе первого порядка