Численные методы решения обыкновенных дифференциальных уравнений и систем: Методические указания к курсовой работе, страница 14

3.3. Системы уравнений первого порядка

Решить задачу Коши для системы дифференциальных уравнений первого порядка при различных начальных условиях. Величину интервала решения и шаг подобрать самостоятельно, так чтобы решение не выходило за пределы сотен единиц и давало картину поведения траекторий. Решить задачу на отрезке  [0,T]

1.  Проверить устойчивостьмодели хищник – жертвапо отношению к начальным условиям, Для этого изменить начальные условия    на 2 единицы в каждом направлении (четыре различных случая) и получить решение методом Рунге-Кутта. Значения прочих параметров взять из примера, выполненного в методических указаниях

2.  Проверить чувствительность модели хищник – жертва по отношению к параметрам уравнения, рассматривая изменение параметра    на  0.01  в сторону увеличения и уменьшения, а также изменение параметра    на  0.002  в ту и другую сторону.

3.  Рассмотреть модель хищник – жертва  при условии, что в уравнение для числа жертв включен член, выражающий самоподавление вида, состоящее в том, что число жертв уменьшается пропорционально квадрату их количества, т. е. система уравнений, описывающая популяции, имеет вид:

                  

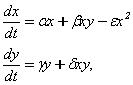
где 

Значения ранее рассмотренных параметров и  начальные условия взять из примера методических указаний. Положить e=0.001. Исследовать поведение на различных временных отрезках.

4.  Решить систему уравнений

                         

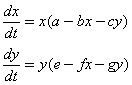
при положительных значениях, входящих в него коэффициентов   

5.  Рассмотреть модель хищник – жертва  при условии, что в уравнение для числа жертв включен член, выражающий взаимопомощь членов первого вида, благодаря которой  число жертв увеличивается пропорционально квадрату их количества, т. е. система уравнений, описывающая популяции, имеет вид:

                  

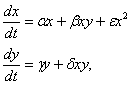
где 

Значения ранее рассмотренных параметров и  начальные условия взять из примера методических указаний. Положить e=0.001. Исследовать поведение на различных временных отрезках.

6.  Решить систему уравнений, описывающую взаимодействие двух видов, причем скорость прироста каждого вида пропорциональна их количеству с положительными коэффициентами и количеству каждого вида с отрицательными коэффициентами. Положить в уравнении (1.2)     .

Вектор начальных условий подобрать самостоятельно.

7.  Рассмотреть модель хищник – жертва  при условии, что в уравнение для числа жертв включен член, выражающий взаимопомощь членов первого вида, благодаря которой  число жертв увеличивается пропорционально квадрату их количества, т. е. система уравнений, описывающая популяции, имеет вид:

                  

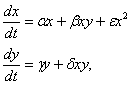
где 

Значения ранее рассмотренных параметров и  начальные условия взять из примера методических указаний. Положить e=0.001. Исследовать поведение на различных временных отрезках.

8.  Рассмотреть модель хищник – жертва  при условии, что в уравнение для числа жертв включен член, выражающий взаимопомощь членов второго вида, благодаря которой  число хищников увеличивается пропорционально квадрату их количества, т. е. система уравнений, описывающая популяции, имеет вид: