Численные методы решения обыкновенных дифференциальных уравнений и систем: Методические указания к курсовой работе, страница 6

4. Вычисление третьего столбца:

Копируем формулу из ячейки C3 в ячейки C4:C17

5.  Вычислим в узловых точках отрезка [a, b] аналитическое решение по формуле (2.2). Для этого введем в ячейку F3 формулу

      =$B$3*EXP($E$3*A4). Затем копируем ее в ячейки  F4:F18

Расчетная таблица, скопированная с рабочего листа MS Excel, показана на рис. 2.1.

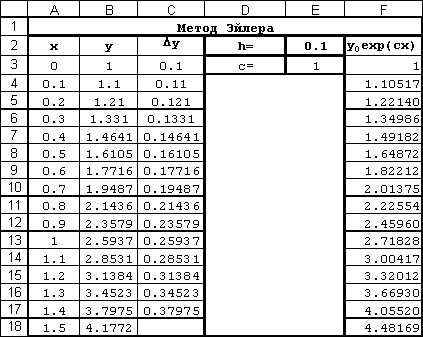
Рис. 2.1. Фрагмент рабочего листа с решением примера методом Эйлера

2.1.4.Численное решение методом Рунге-Кутта в Excel

Расчетные формулы для конкретного примера запишем, исходя из общих формул и подставляя в них конкретные функции, определяемые видом уравнения (2.1). Отметим, что исходное уравнение должно быть приведен к виду (1.1).

Задаемся начальным значением y₀   и вычисляем

,         (2.6)

                                                          (2.7)

Приведем также пример расчетных формул для уравнения другого вида, а именно уравнения, содержащего  x  в правой части.

Рассмотрим уравнение

Для него расчетные формулы имеют вид:

 

Расчетная таблица, скопированная из Excel, представлена на рис. 2.2. Ниже указан порядок ее заполнения

Первая строка заполнена именами переменных

Две ячейки H21, H22 отводятся под значения констант h, c и еще две ячейки G21?G22 под их имена

Первый столбец заполняется значениями x

В ячейку B22 вводим значение y₀,

В ячейки С22,D22, E22, F22 вводим соответственно формулы:

= $H$22*B22*$H$21

=$H$22*(B22+C22/2)*$H$21

=$H$22*(B22+D22/2)*$H$21

=$H$22*(B22+E22)*$H$21

В ячейку B23 вводим формулу:

=B22+(C22+2*D22+2*E22+F22)/6

В ячейки B24:B37 копируем формулу из ячейки B23

В ячейки C22:F36 копируем формулы из ячеек C22:F22.

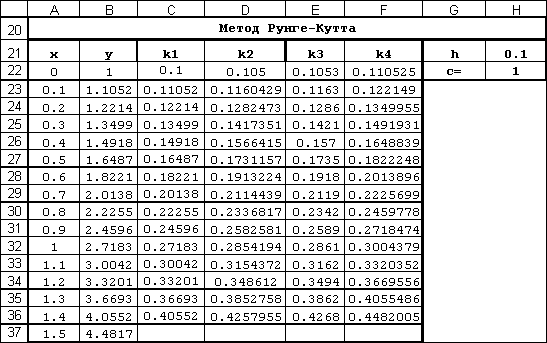
Рис. 2.2. Фрагмент рабочего листа с решением примера по методу Рунге-Кутта

Построим графики численного решения данного уравнения в Excel методами Эйлера и Рунге-Кутта, а также график аналитического решения. Все три графика строим на одной диаграмме. При построении графика с помощью Мастера диаграмм следует:

1.  На первом шаге  выбрать Тип диаграммы - Точечная

2.  На втором шаге последовательно задать ряды данных для каждого графика:

3.  На третьем шаге задать параметры Диаграммы:  заголовок, названия осей. В  случае абстрактного уравнения заголовок диаграммы можно опустить. В легенде следует указать, какому методу данный ряд соответствует.

4.  На последнем шаге помещаем диаграмму на имеющемся рабочем листе.

Примечания.

1.  Если графики трудно различимы, можно изменить  формат рядов данных (на графике), выделяя соответствующий ряд и вызывая контекстное меню правой кнопкой мыши

2.  Если шкалы по осям x или y не соответствуют диапазону изменения x, y, нужно изменить их минимальные и максимальные значения по команде формат оси, вызываемой в контекстном меню.

Графики решения данного уравнения различными методами представлены на рис. 2.3.

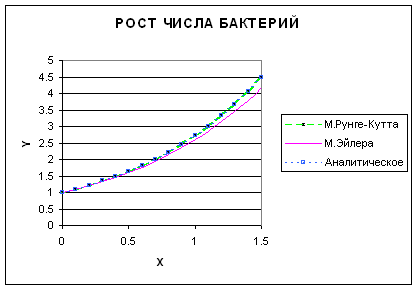
Рис. 2.3. Графики решений уравнения (2.1) различными способами

2.1.5. Численное решение задачи методом Рунге-Кутта в Турбо Паскале

Расчетные формулы.

Решим уравнение (2.1) методом Рунге-Кутта четвертого порядка, используя формулы (1.8)-(1.9). Т.к. неизвестные значения функции y(x)  вычисляются рекуррентно, требуется задать ее начальное значение.