Значения параметров ![]()
Если при вводе параметров на экран выводится подсказка к вводу, следует остается набрать соответствующие значения вводимых переменных.
Результаты расчета должны выводяться в файл
Содержимое выходного файла (файла результатов) для данного примера:
Число точек деления
n=20
Промежуток интегрирования
A=x0= 0.00 b=10.00
Начальные значения функций y0, z0
80 30
Параметры уравнения
al= 0.25 be= -0.01 gam= -1.00 del= 0.01
Таблица 2.3
____________________________
x y z
____________________________
0.00 80.00000 30.00000
0.50 78.60834 27.03736
1.00 78.36068 24.26878
1.50 79.14334 21.81389
2.00 80.84705 19.73045
2.50 83.37126 18.03635
3.00 86.62169 16.72811
3.50 90.50424 15.79455
4.00 94.91629 15.22626
4.50 99.73606 15.02197
5.00 104.81017 15.19266
5.50 109.93986 15.76377
6.00 114.86755 16.77483
6.50 119.26757 18.27463
7.00 122.74887 20.30817
7.50 124.88152 22.89107
8.00 125.26032 25.96890
8.50 123.60926 29.36908
9.00 119.90367 32.77082
9.50 114.45120 35.73185
10.00 107.86486 37.79394
10.50 100.91430 38.63228
11.00 94.32622 38.16470
11.50 88.63666 36.55674
12.00 84.14654 34.13390
12.50 80.95956 31.26541
13.00 79.05166 28.27631
13.50 78.33388 25.40679
14.00 78.69451 22.80920
14.50 80.02139 20.56469
15.00 82.21026 18.70551
15.50 85.16477 17.23528
16.00 88.79167 16.14470
16.50 92.99314 15.42267
17.00 97.65691 15.06388
17.50 102.64460 15.07374
18.00 107.77836 15.47144
18.50 112.82697 16.29082
19.00 117.49417 17.57775
19.50 121.41505 19.38114
20.00 124.17078 21.73314
____________________________
Для анализа результатов представим их в графической форме. Построим так называемую траекторию решения, а именно график зависимости одной искомой функции от другой. В общих обозначениях это зависимость z от y. Мы исключили из рассмотрения время, которое в данном случае является параметром.
С этой целью результаты, полученные на экране, переносятся в таблицу EXCEL, и по ним строится точечная диаграмма. По графику можно проследить изменение численности жертв и хищников во времени при движении вдоль кривой. Вначале количество жертв растет, а число хищников уменьшается, затем начинается восстановление популяции хищников, при этом число жертв какое-то время почти не меняется, а потом начинает уменьшаться. График зависимости z от y показан на рис. 2.6.
Отметим некоторые качественные особенности решения, показанного на рис. 2.6. Рассмотренная система имеет стационарную точку. Стационарной точкой называется точка в пространстве решений, в которой правые части всех уравнений обращаются в нуль. Если в качестве начальных значений неизвестных функций взять координаты стационарной точки, то легко понять, что в этом случае значения неизвестных функций остаются постоянными в силу равенства нулю их производных. Если начальные условия близки к стационарной точке, то, как правило, решение совершает колебания вблизи этой точки или приближается к ней.
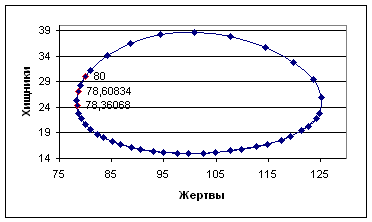
Рис. 2.6. Траектория решения при указанных исходных данных
Графики зависимости популяций от времени показаны на рис. 2.7.
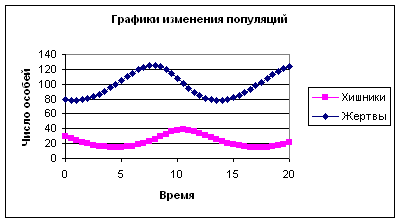
Рис. 2.7 Зависимость численности видов от времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.