Погрешности датчика угловой скорости, инструментальная погрешность, страница 6

Согласно принципу суперпозиции

в случае, когда амплитуда A=C, а B=D.

Применив принцип суперпозиции к выражению (13.18), получим:

Совместное решение уравнений (13.19) позволяет найти выражения для амплитуды A и фазы e вынужденных колебаний:

Обозначим через  амплитуду вынужденных колебаний при частоте возмущения =0. Назовем амплитуду  амплитудой измерения в динамическом режиме (¹0). Под динамическим режимом будем понимать режим, при котором измеряемый параметр изменяется во времени с определенной частотой. Если измеряемый параметр на определенном временном интервале не изменяется во времени, то такой режим называют статическим. Амплитуда  измеряемого параметра при =0 называется амплитудой статического режима. Характеристикой амплитуды  в динамическом режиме является коэффициент динамической восприимчивости :

.

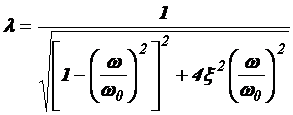В теории автоматического регулирования коэффициент  носит название относительной амплитудно-частотной характеристики.