М-11. МЕТОД ПЕРЕМЕЩЕНИЙ
11.0. Введение в модуль
Основными целями модуля являются:
- рассмотрение понятия степени кинематической неопределимости;
- получение формул для определения внутренних усилий в произвольной плоской статически неопределимой раме;
- рассмотрение особенностей определения внутренних усилий с учетом симметрии плоской статически неопределимой рамы;
- рассмотрение особенностей применения метода перемещений к плоским статически неопределимым рамам с ригелями повышенной из- гибной жесткости;
- рассмотрение особенностей определения внутренних усилий в плоских статически неопределимых несвободных рамах при действии уз- ловой нагрузки.
Структура изучаемого модуля включает следующие учебные элементы:
1. Расчет плоских статически неопределимых рам методом перемещений.
2. Использование свойств симметрии при расчете рам методом перемещений.
3. Особенности применения метода перемещений к рамам с ригелями повышенной изгибной жесткости.
4. Особенности определения внутренних усилий в несвободных рамах при действии узловой нагрузки.
При изучении учебных элементов рекомендуется использование следующей литературы: [1, c.391 – 448]; [3, c.265 – 302]; [4, c.365 – 378];
[5, c. 372 – 404].
11.1.Расчетплоских статически неопределимых рам методом перемещений
11.1.1.Суть метода и его допущения
Расчет статически неопределимой рамы методом сил начинается с определения ее степени статической неопределимости, которая равняется числу лишних связей в системе, и нахождения основных неизвестных, ко-
торыми являются внутренние усилия, возникающие в этих связях. После этого легко определяются и остальные внутренние усилия. Зная же внут- ренние усилия, можно найти перемещения в любом месте рамной системы.
Однако наряду с порядком расчета рамы, когда сначала определяются внутренние усилия, а затем находятся перемещения, возможен и иной порядок определения этих величин. Если для некоторой рамной конструк- ции каким-либо образом найти ее узловые перемещения (линейные и угло- вые), то после этого нетрудно будет найти и все внутренние усилия в стержнях системы. Такой порядок расчета стержневой системы и состав- ляет сущность метода перемещения. Узловые перемещения, подлежащие первоочередному определению, являются основными неизвестными ме- тода перемещений, а их общее число и называется степенью кинемати- ческой неопределимости n. Сама же стержневая система считается кине- матически неопределимой.
При определении степени кинематической неопределимости в рамах вводятся два допущения. Во-первых, пренебрегают продольными и попе- речными деформациями стержней, поскольку при определении перемеще- ний в рамных системах, как правило, учитываются только деформации из- гиба. И, во-вторых, ввиду малости перемещений в линейно деформируе- мых системах, пренебрегают сближением концов изгибаемых стержней. Введение указанных допущений позволяет не учитывать при расчете вто- ростепенные перемещения и, следовательно, уменьшать степень кинема- тической неопределимости.
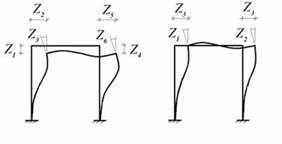
Рис. 11.1
Пример, приведенный на рис.11.1, показывает, что, с учетом принятых до- пущений, степень кинематической неопределимости рамы уменьшилась в два раза.
Степень кинематической неопределимости произвольной плоской рамы определяется по формуле
n = n1 + n2 ,
где
n1 - число неизвестных угловых перемещений узлов рамы,
n2 - число
неизвестных линейных перемещений узлов рамы, которое характеризует степень линейной подвижности рамы.
Число неизвестных угловых перемещений
n1 равняется числу жест-
ких узлов рамы. Для определения степени линейной подвижности рамы n2
во все жесткие узлы рамы вводятся шарниры. Число степеней свободы, полученной шарнирно стержневой системы, совпадает со степенью линей- ной подвижности рамы. Следовательно, для рамы, показанной на рис.11.2,
n2 = 1.
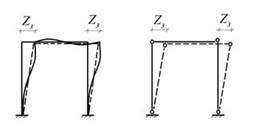
Рис. 11.2
Рамы, у которых могут возникать линейные перемещения узлов
только за счет изгибных деформаций ее стержней
n2 ¹ 0 , принято называть
свободными рамами. Рамы, у которых такие перемещения отсутствуют
n2 = 0 , называются несвободными рамами.
11.1.2.Постановказадачи
Задана произвольная плоская статически и кинематически неопределимая рама (рис. 11.3)
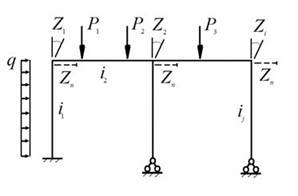
Рис. 11.3
Степень кинематической неопределимости рамы характеризуется величи-
нами
n, n1 ¹ 0,
n2 ¹ 0 , которые определяются в соответствии с неизвестны-
ми узловыми перемещениями
Z1 ,...,Zn . Для рамы считаются известными
геометрические размеры расчетной схемы, геометрические характеристики
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.