Метод перемещений, страница 2

поперечных сечений стержней и их конструкционный материал. В преде- лах каждого стержня геометрические характеристики поперечного сечения считаются  постоянными.  Способность  произвольного  стержня  рамы  со- противляться изгибным деформациям будем описывать величиной погон- ной жесткости

(EI )

i  =          j

j

На раму действуют произвольная нагрузка. Заданная конструкция считается линейно деформируемой системой.

11.1.3.Основная система и канонические уравнения

В  основе  расчета  рам  методом  перемещений  лежит  переход  от  за- данной  кинематически  неопределимой  системы  к  расчету  эквивалентной кинематически определимой системе. Эквивалентность двух систем должна состоять в одинаковости перемещений (кинематическая эквивалент- ность метода перемещений) и одинаковости  внутренних усилий (стати- ческая  эквивалентность  метода  перемещений).  Такая  эквивалентная система и называется основной системой метода перемещений.

Для получения основной системы из заданной на узлы рамы накла- дываются  дополнительные  связи,  которые  исключают  возможность  воз- никновения угловых и линейных перемещений ее узлов (рис. 11.4).

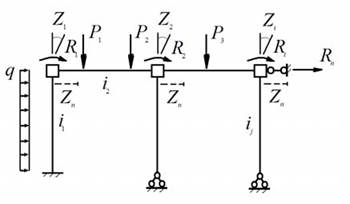
Рис. 11.4

Для исключения угловых перемещений на все жесткие узлы накладываются связи, исключающие их повороты. Такие связи для краткости будем на- зывать «шайбами» и изображать в виде квадрата, окаймляющего жесткий узел.  Для  исключения  линейных  перемещений  на  узлы  по  направлению этих перемещений накладываются стержни. Преобразованная таким обра-

зом система состоит из отдельных статически неопределимых балок, в ней отсутствуют все узловые перемещения и, следовательно, она является ки- нематически определимой системой.

Кинематическая  эквивалентность  полученной  кинематически  оп- ределимой  системы  заданной  системе  достигается  приложением  к  ней  в качестве  дополнительных  внешних воздействий  неизвестных  узловых пе-

ремещений

Z1 ,...,Zn

(рис. 11.4). При дальнейшем расчете эти перемещения

подлежат  первоочередному  определению  и  поэтому  они  называются  ос- новными  неизвестными  метода  перемещений.  И,  поскольку,  основные неизвестные  являются  перемещениями,  то  они  имеют  кинематическую природу.

Для  достижения  статической  эквивалентности  двух  систем  вводятся условия обращения в ноль реакций (рис. 11.4)

R1  = 0,...,Rn   = 0 ,                                        (11.1)

возникающих в кинематически определимой системе в наложенных связях по  направлению  основных  неизвестных.  И  так  как  эти  реакции  порожда- ются    основными  неизвестными  и  заданной  внешней  нагрузкой,  то  они являются функциям этих величин и условия (11.1) можно записать в сле- дующем виде

R (Z,...,Z

,P ) = 0,

1        1         n

..............................

(11.2)

R (Z,...,Z

,P ) = 0.

n1         n

Поскольку заданная стержневая  конструкция считается линейно деформируемой      системой,     то   дополнительные       условия     (11.2),    согласно принципу суперпозиции, принимают вид

+ R1P   = 0,

.....................................

(11.3)

+ ...+ RnZ

+ RnP   = 0.

Входящие  в  (11.3)  величины  имеют  следующий  смысл:

(i , j = 1,...,n)  -

реакция в наложенной связи основной системы по направлению основного

неизвестного   №   i,   вызванная   действием   основного   неизвестного

Z j ;