Метод перемещений, страница 4

только к ней, то для построения единичных и грузовых эпюр изгибающих моментов  и  поперечных  сил  основной  системы  используют  единичные  и грузовые  эпюры,  построенные  для  отдельных  балок.  В  таблице  11.1  для некоторых случаев нагружений однопролетных балок постоянного сечения приводятся единичные и грузовые эпюры изгибающих моментов и значе- ния  опорных  реакций.  Знание  этих  реакций  позволяет  достаточно  просто для каждого типа балки получить очертание соответствующих эпюр попе- речных сил

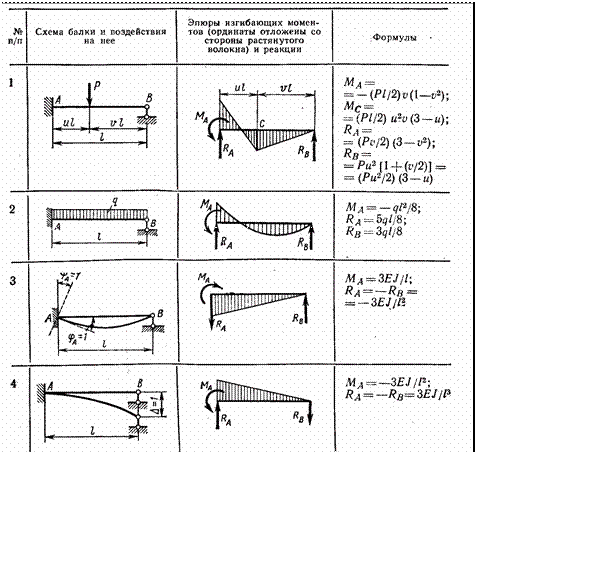Таблица 11.1

После  рассмотрения  единичных  и  грузового  состояний  основной системы и построения, соответствующих им эпюр изгибающих моментов и поперечных сил, осуществляется вычисление коэффициентов и свободных членов канонических уравнений. Их вычисление может производиться ста- тическим способом или способом перемножения эпюр. На практике обычно применяют первый способ, который более прост. Способ перемножения эпюр  целесообразно  применять  при  расчете  рам  с  наклонными  элемента- ми.

Суть  статического  способа  заключается  в  вырезании  сквозными  се- чениями узлов и отдельных частей основной системы и определении реак- ций в наложенных связях из условий равновесия вырезанных частей. Такое вырезание  производится  в  бесконечной  близости  от  центров  узлов.  При этом значения изгибающих моментов и поперечных сил в сечениях пере- резанных стержней берутся из соответствующих им эпюр. Схемы опреде- ления двух коэффициентов статическим методом для рассмотренного еди- ничного состояния приведены на рис.11.5,в.

11.1.5.Решениеканоническихуравнений

Математической  формой  канонических  уравнений  метода  переме- щений, как и в случае метода сил, является система неоднородных линей- ных алгебраических уравнений

a11 x1  + a12 x2  + ... + a1n xn   = b1

a21 x1  + a22 x2  + ... + a2 n xn   = b2  ,

......................................

an1 x1  + an 2 x2  + ... + ann xn   = bn

где

aij   = rij ,x j   = Zj ,bi   = -RiP . Поэтому для решения канонических уравнений

метода перемещений применяют те же численные методы решения  систем линейных алгебраических уравнений, что и в случае метода сил.

11.1.6.Определение внутренних усилий заданной системы

Для определения внутренних усилий, которые возникают в заданной системе от приложенных к ней внешних воздействий, используется основ- ная система метода перемещений и результаты ее расчета следующим об- разом.

При  нахождении  коэффициентов  канонических  уравнений

rij

к  ос-

новной системе прикладывались перемещения

Z= 1 ( j = 1,...,n)

и   для ка-

ждого  загружения  были  получены  единичные  внутренние  усилия

mj ,qj .

Поскольку  приложенные  к  основной  системе  в  качестве  дополнительных

внешних воздействий основные неизвестные

Z1 ,...,Zn

найдены и основная

система  считается  линейно  деформируемой,  то  изгибающие  моменты  и

поперечные силы, возникающие в ней от действия

Z1 ,...,Zn , будут равны

MZ   = m1Z1  + ...+ mn Zn ,

QZ   = q1Z1  + ...+ qn Zn .

(11.6)

RiP

При     определении      свободных      членов     канонических       уравнений

(i = 1,...,n) к основной системе прикладывалась заданная нагрузка, и бы-

ли найдены грузовые внутренние усилия

M P ,QP  .

Таким  образом,  для  определения  изгибающих  моментов  и  поперечных сил в заданной системе необходимо, в соответствии с принципом суперпозиции, сложить внутренние усилия, полученные в основной системе

от  основных  неизвестных

Z1 ,...,Zn

и  заданной  нагрузки.  Следовательно,

формулы для определения изгибающих моментов и поперечных сил имеют вид

M= m1Z1  + ...+ mn Zn  + MP ,

(11.7)