Метод перемещений, страница 6

11.4. Особенности определения внутренних усилий в несвободных рамах при действии узловой нагрузки

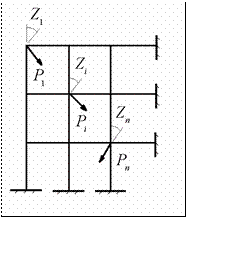Рассмотрим некоторую n- раз кинематически неопределимую несво- бодную  раму,  нагруженную  в  узлах  произвольными  сосредоточенными силами (рис.11.12)

Рис.11.12

В этом случае степень кинематической неопределимости порождается не-

известными углами поворота жестких узлов рамы

Z1 ,...,Zn .

Тогда основная система метода перемещений образуется наложени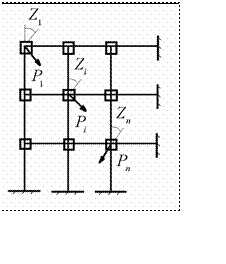ем шайб на все жесткие узлы рамы (рис.11.13)

Рис.11.13

а соответствующие ей канонические уравнения имеют вид

r11Z1  + ...+ r1nZn+ R1P= 0,

......................................

rn1Z1  + ...+ rnnZn+ RnP= 0.

(11.8)

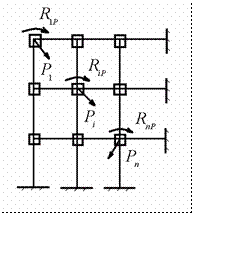Рассмотрим, какие особенности возникают при определении свобод- ных членов системы (11.8). Так как при действии узловой нагрузки на ос- новную систему (рис.11.14)

Рис.11.14

ни один из ее элементов не изгибается, то изгибающие моменты, и попе- речные  силы  грузового  состояния  в  любом  сечении  основной  системы имеют нулевые значения

M P   º 0,

QP   º 0

(11.9)

Тогда из условия равновесия узлов основной системы следует, что все свободные члены также имеют нулевые значения нулю

RiP   º 0

(i = 1,...,n)

(11.10)

вид

С учетом (11.10) система канонических уравнений (11.8) принимает

r11Z1  + ... + r1n Zn   = 0,

..............................

rn1Z1  + ... + rnn Zn   = 0.

и представляет  собой относительно основных неизвестных систему одно- родных  линейных  алгебраических  уравнений.  С  учетом  положительной определенности  определителя                         матрицы                              коэффициентов                  канонических уравнений  метода  перемещений  такая  система  имеет  единственное  реше- ние

Zi   º 0

(i = 1,...,n) .                                 (11.11)

Полученное  решение  (11.11)  означает,  что  при  действии  на  несвободные рамы произвольной узловой нагрузки ни один из ее жестких узлов не по- ворачивается.

Тогда из формул (11.7) с учетом (11.9) и (11.11), следует, что изгибающие моменты, и поперечные силы в произвольном сечении любой несвободной рамы при узловой нагрузке имеют нулевые значения

M  º 0,

Q º 0 .

а  действующая  нагрузка  уравновешивается,  возникающими  в  стержнях рамы продольными силами.

Для  определения  продольных  сил  достаточно  рассмотреть  равнове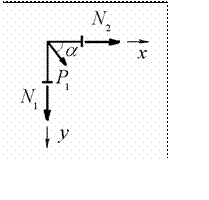сие узлов и составить уравнения проекций на координатные оси. Начинать рассмотрение  равновесия  нужно  начинать  с  узла,  где  сходится  не  более двух стержней с неизвестными продольными силами (рис.11.15)

Рис.11.15

Уравнения равновесия для узла, показанного на рис.12.15, имеют вид

å y = 0;

å x = 0;

N1  + P1 sina = 0

N2  + P1 cosa = 0

Решая эти уравнения, находим значения продольных сил в стержнях, примыкающих к данному узлу

Из  полученных  формул  для  продольных  сил  следует,  что  они  постоянны по длине каждого стержня и могут меняться только для различных стержней.

Поскольку рассматриваемая рама является несвободной, то она оста- ется  геометрически  неизменяемой  при  условной  замене  жестких  узлов шарнирными. При этом очевидно, что в составляемых уравнениях равно- весия для узлов ничего не изменяется. Поэтому для определения продоль- ных сил в стержнях несвободных рам при действии узловой нагрузки мо- жет  использоваться  шарнирно-стержневая  система,  получаемая  из  задан- ной несвободной рамы при условной замене жестких узлов шарнирными.

Сделанный  вывод  позволяет  вернуться  к  вопросу  о  правомерности использования шарнирных узлов при расчете ферм. Реальная ферма, строго говоря, является несвободной рамной конструкцией. Поэтому при узловой  схеме  нагружения  во  всех  стержнях  фермы  изгибающие  моменты  и поперечные  силы  равны  нулю,  а  продольные  силы  постоянны  по  длине каждого стержня. И при их определении жесткие узлы фермы могут заме- няться шарнирными. Однако следует помнить, что это справедливо только