Метод перемещений, страница 3

RiP

(i = 1,...,n)

- реакция в наложенной связи основной системы по направ-

лению основного неизвестного № i , вызванная действием нагрузки.

RiZ   и основного неизвестного

Z j    связа-

ны прямой пропорциональной зависимостью, то

= rij Z j ,                                                 (11.4)

где

rij

- единичная реакция в наложенной связи основной системы по на-

правлению основного неизвестного № i   от действия безразмерного пере~

мещения

Zj   = 1.

С учетом (11.4) соотношения (11.3) принимают вид уравнений

r11Z1  + ... + r1nZn+ R1P= 0,

......................................

rn1Z1  + ... + rnnZn+ RnP= 0.

(11.5)

Полученные уравнения (11.5) представляют собой систему неоднородных линейных алгебраических уравнений относительно основных неизвестных

Z1 ,...,Zn

и  называются  каноническими  уравнениями  метода  перемеще-

ний.  Они  имеют  статическую  природу,  так  как  каждое  такое  уравнение выражает равенство нулю реакции в наложенной связи основной системы по направлению основного неизвестного, номер которого совпадает с но- мером соответствующего уравнения, от действия всех основных неизвест- ных и нагрузки.

Входящие в эти уравнения единичные реакции

rij

в качестве множи-

телей  при  основных  неизвестных  называются  коэффициентами  канони- ческих уравнений метода перемещений. В зависимости от соотношений между индексами различают два вида таких коэффициентов. В случае если

i =  j ,  то  соответствующие  коэффициенты  называются  главными  коэф-

фициентами, и они удовлетворяют условию строгой положительности

rii

> 0 (i = 1,...,n).

В  случае  если

i ¹  j ,  то  соответствующие  коэффициенты  называются  по-

бочнымикоэффициентами, и они удовлетворяют условию взаимности

rij

= rji

(i , j = 1,...,n) .

Входящие в канонические уравнения реакции

RiP

(i = 1,...,n) от дейст-

вия  нагрузки  называются  свободными  членами  канонических  уравне-

ний метода перемещений.

11.1.4.Определение коэффициентов  и свободных членов

Для  определения  коэффициентов  канонических  уравнений  метода перемещений нужно последовательно загрузить основную систему безраз-

мерными перемещениями

Z= 1 ( j = 1,...,n) . Такие схемы нагружения счи-

таются  единичными  состояниями  основной  системы  метода  переме-

щений. Пример образования единичного состояния приведен на рис. 11.5,а

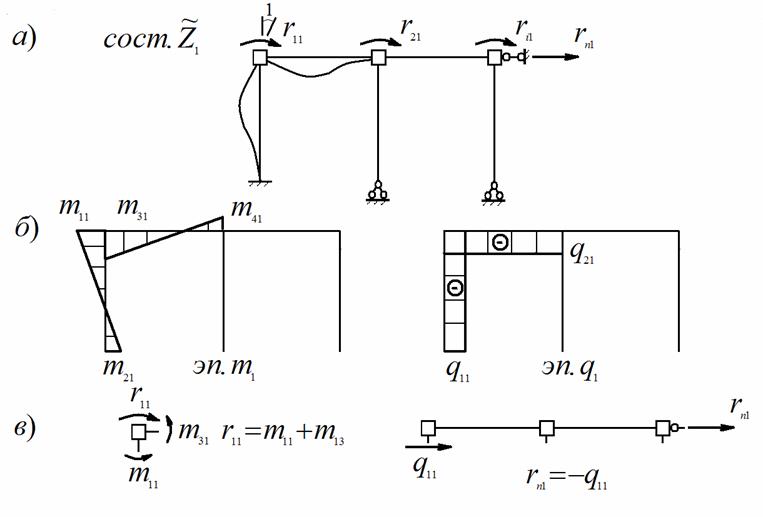
Рис.11.5

Построенные для каждого  единичного состояния эпюры  изгибающих  мо-

ментов  m j

и  поперечных  сил

qj  называются  единичными  эпюрами  этого

состояния основной системы (рис. 11.5,б).

Для    определения       свободных       членов     канонических       уравнений

RiP

(i = 1,...,n)

необходимо  рассмотреть  основную  систему  под  действием

нагрузки и построить эпюры изгибающих моментов  M P

и поперечных сил

QP . Такие эпюры

M P ,  QP

называются грузовыми, а соответствующая им

схема нагружения считается грузовым состоянием основной системы.

Поскольку  основная  система  представляет  собой  совокупность  ста- тически неопределимых балок с различными закреплениями концов, и ка- ждая  из  таких  балок  воспринимает  внешние  воздействия,  приложенные