Метод перемещений, страница 5

Q= q1Z1  + ...+ qn Zn  + QP .

Продольные силы, при известных поперечных силах, определяются из условия равновесия узлов заданной системы.

11.2.Использованиесвойствсимметриипри расчете рам методом перемещений

Выясним особенности использования свойств симметрии при расчете рам методом перемещений на частном примере. Рассмотрим одноэтаж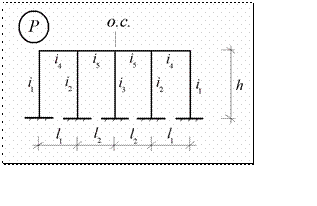ную четырехпролетную раму (рис.11.6)

Рис.11.6

Геометрические и жесткостные параметры рамы удовлетворяют признакам симметрии,  и  рама  обладает  осью  симметрии.  На  раму  действует  произ-

вольная  нагрузка, показанная  на рис.11.6 условным буквенным  обозначением P .

Рассматриваемая рама 6 раз кинематически неопределимая и степень кинематической  неопределимости  характеризуется  пятью  угловыми  пере-

мещениями

Z1 ,...,Z5

и  одним  линейным  перемещением

Z6 ,  являющихся

основными  неизвестными  метода  перемещений  данной  рамы.  Основная система  метода  перемещений,  связанная  с  их  определением,  имеет  вид (рис.11.7)

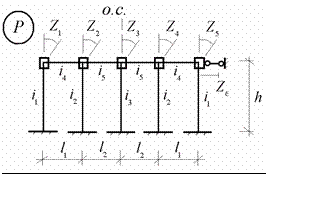Рис.11.7

Так как основные неизвестные не удовлетворяют признакам симмет- рии,  то  их  определение  связано  с  составлением  и  совместным  решением шести канонических уравнений

r11Z1  + ...+ r16 Z6  + R1P   = 0,

......................................

r61Z1  + ...+ r66 Z6  + R6 P   = 0.

Получение симметричных и антисимметричных  основных неизвестных, также как и при расчете методом сил, связано с использованием прием группировки однотипных основных неизвестных. Для рассматриваемой

рамы выделяются две пары таких величин -   углы поворота

Z1 ,  Z5

и углы

поворота

Z2 ,

Z6 ,  которые  искусственно  разделяются  на  симметричные  и

антисимметричные       составляющие.       Эти    искусственно      выделенные                                   две группы  величин  перемещений  и  являются  новыми  основными  неизвест- ными,  соответственно,  симметричными  и  антисимметричными.  Два  ос-

тавшихся исходных перемещения  Z3

и  Z6 , связанных с антисимметричной

схемой  деформирования  рамы,  целиком  относятся  к  новым  антисимметричным основным неизвестным.

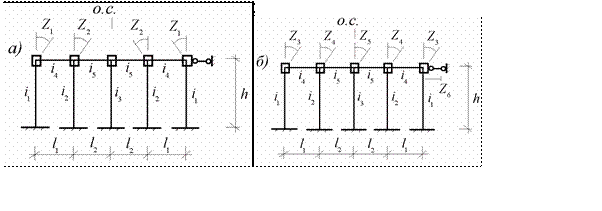Для определения новых основных неизвестных рассматривается два состояния  основной  системы  –  симметричное  (рис.11.8.а)  и  антисиммет- ричное (рис.11.8.б)

Рис.11.8

Тогда исходная система канонических уравнений распадается на две независимые подсистемы уравнений. Первая подсистема уравнений

r11Z1  + r12 Z2  + R1P= 0,

r21Z1  + r22 Z2  + R2 P= 0.

позволяет найти симметричные основные неизвестные. Вторая подсистема уравнений

r33 Z3  + r34 Z4  + r35 Z5  + r36 Z6  + R3 P= 0,

r43 Z3  + r44 Z4  + r45 Z5  + r46 Z6  + R4 P= 0,

r53 Z3+ r54 Z4  + r55 Z5  + r56 Z6  + R5 P= 0,

r63 Z3  + r64 Z4  + r65 Z5  + r66 Z6  + R6 P= 0

позволяет найти антисимметричные основные неизвестные.

11.3. Особенности применения метода перемещений к рамам

с ригелями повышенной изгибной жесткости

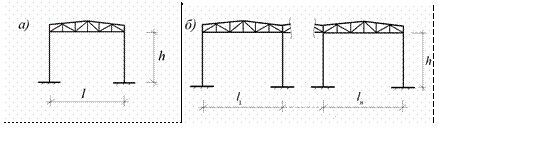
Поперечной  несущей  конструкцией  цехов  одноэтажных  промыш- ленных  зданий  обычно  является  плоская  однопролетная  (рис.11.9.а)  или многопролетная рама (рис.11.9.б)

Рис.11.9

Ригелями  в  таких  рамах,  как  правило,  являются  фермы,  изгибная  жесткость которых в пять и более раз превышает изгибную жесткость колонн.

В этом случае при расчете поперечных рам на действие горизонталь- ных  нагрузок  можно  пренебречь  изгибом  ригеля  и  приближенно  считать изгибную жесткость ригеля бесконечно большой величиной. Подобное до- пущение  существенно  упрощает  применение  метода  перемещений  для расчета таких рам.

С учетом принятого допущения расчетная схема рамного поперечника в случае одного пролета имеет вид, показанный на рис.11.10.а, и в слу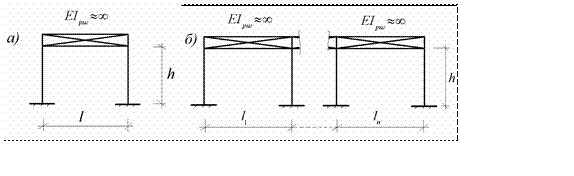чае нескольких пролетов - показанный на рис.11.10.б

Рис.11.10

В  обоих  случаях  у  рам  отсутствуют  угловые  перемещения.  Поэтому  сте- пень кинематической неопределимости рам порождается одним неизвест- ным горизонтальным перемещением узлов и равняется единице.

Тогда основная система метода перемещений, как в случае однопро- летной, так и в случае многопролетной рам образуется наложением одного стержня, препятствующего линейному горизонтальному перемещению уз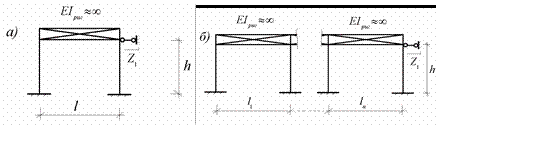лов рам (рис.11.11)

Рис.11.11

Следовательно,  для  расчета  рам  методом  перемещений  при  любом  числе пролетов достаточно составить одно каноническое уравнение

r11Z1  + R1 P   = 0 .