по строительной механике
Выполнил студент группы
06-ПГС-5 Асташева Г.В.
Проверил преподаватель
Синявская Н.В.
Новополоцк – 2009
«РАСЧЕТ ПЛОСКОЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ МЕТОДОМ СИЛ»
Раскрыть статическую неопределимость симметричной рамы, выделить, симметричную и антисимметричную составляющие нагрузки и для симметричной составляющей нагрузки определить внутренние усилия и построить эпюры М, Q, N.
Таблица 1 - Исходные данные к контрольной работе №1
|
№ группы |
№ п/п |
Сосредоточенные нагрузки, кН |
Распределенные нагрузки, кН/м |
Размеры, м |
a |
b |
J2 J1 |
||||
|
Р1 |
Р2 |
q1 |
q2 |
q3 |
l |
h |
|||||
|
1 |
2 |
- |
22 |
8 |
- |
12 |
6 |
4 |
0.9 |
0.5 |
1.5 |
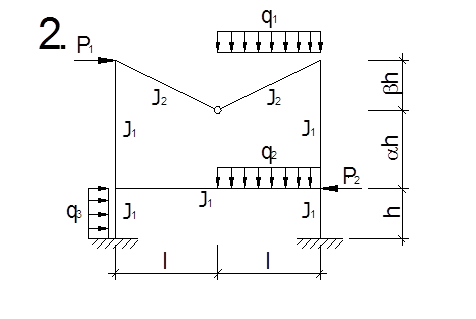
1. Кинематический анализ.
1.1. Изображаем расчетную схему рамы в виде кинематической цепи (рис.1).
Число дисков Д=1;
Число узлов У=0;
Число шарниров Ш=0;
Число стержней С=0;
Число опорных стержней С0=6;
1.2. Подсчитаем число степеней свободы W.
W=3Д+2У-2Ш-С-С0=3-6=-3;
Необходимый признак геометрической неизменяемости выполнен.
1.3. Выполним анализ геометрической структуры.
Диск Д1 крепится к «земле» при помощи двух жестких заделок и двух стержней. Для неподвижного присоединения к «земле» достаточно даже только одной жесткой заделки. Система образует с «землей»единый неподвижный диск.
1.4. Следовательно, данная система геометрически неизменяемая и статически неопределима.
1.5. Определим степени полной, внешней и внутренней статической неопределимости.
Степень статической неопределимости Л для системы имеющей замкнутый контур можно по формуле:
Л=-W+3К-Ш.
Число контуров К=2;
Число шарниров Ш=1;
Л=3+3-1=5;
Степень внешней статической неопределимости Л1 определяется из формулы:
Л1=С0-3-Сзам;
Исло «заменяющих стержней Сзам=0;
Л1=6-3=3;
Степень внутренней статической неопределимости Л2 определяется из формулы:
Л2=Л-Л1;
Л2=5-3=2;
Система получилась три раза внешне статически неопределима и 2 раза внутренне статически неопределима.
2. Основная система. Канонические уравнения метода сил.
2.1.Выделим в заданной внешней нагрузке симметричную и антисимметричную составляющие (рис.2).
2.2.Изобразим расчетные схемы вариантов основной системы (рис.3).
2.3. Для дальнейшего расчета используем 1 вариант основной системы и для него выделим симметричные и антисимметричные составляющие в основных неизвестных метода сил (рис.4).
2.4. Запишем канонические уравнения метода сил для симметричной и антисимметричной составляющих внешней нагрузки.
Симметричная составляющая:
Δ1=0; δ11·X1+ δ12·X2 +δ13·X3+ Δ1P=0;
Δ2=0; δ21·X1+ δ22·X2 +δ23·X3+ Δ2P=0;
Δ3=0; δ31·X1+ δ32·X2+ δ33·X3+ Δ3P=0;
Антисимметричная составляющая:
Δ1=0; δ44·X4+ δ45·X5 + Δ4P=0;
Δ2=0; δ54·X4+ δ55·X5 + Δ5P=0;
3. Определение внутренних усилий от антисимметричной составляющей нагрузки
3.1. Рассмотрим основную систему во всех единичных состояниях, соответствующих антисимметричным основным неизвестным и построим эпюры mi, qi, ni (рис.5)
3.2. Определим величину коэффициентов при основных неизвестных метода сил δik.
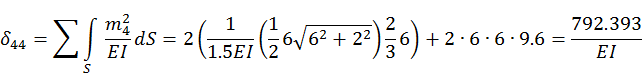
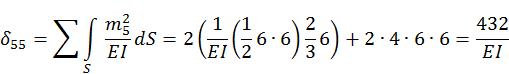
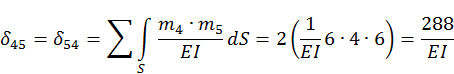
3.3.Проверим правильность вычисления коэффициентов δik.
Для
этого построим суммарную единичную эпюру mAs=m4+m5
и единичные эпюры qAs=q4+q5,
nAs=n4+n5 (рис.6), а затем эту эпюру mAs перемножим саму на себя по правилу Верещагина.
В результате перемножения должны получить сумму всех коэффициентов δik
в системе канонических уравнений метода сил, т.е. проверим равенство:
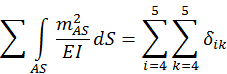
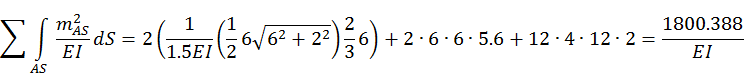
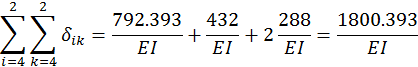
Следовательно, коэффициенты δik при основных неизвестных метода сил найдены правильно.
3.4. Рассмотрим основную систему на действие заданной внешней антисимметричной составляющей нагрузки и построим эпюры Mp.аc., Qp.аc, Np.аc.
Строим эпюры Mp.аc., Qp.аc, Np.аc (рис.7).
3.5. Определим величину свободных членов Δip системы канонических уравнений метода сил для антисимметричной составляющей нагрузки:
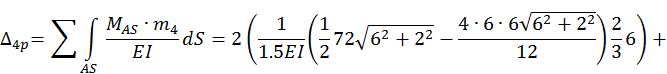
![]()
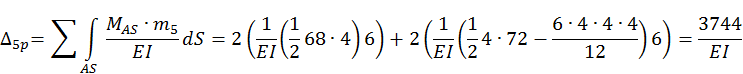
3.6. Проверим правильность определения свободных членов системы канонических уравнений метода сил.
Для этого перемножим эпюру Mp.аc на суммарную единичную эпюру mAS по правилу Верещагина. В результате должны получить сумму всех свободных членов системы канонических уравнений метода сил, т.е.
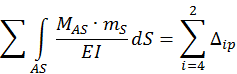
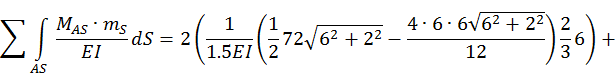
![]()
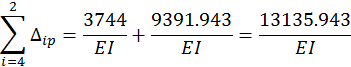
Следовательно, свободные члены определены правильно.
3.7. Подставляем найденные значения δik и Δip в систему канонических уравнений метода сил и решаем ее:
![]()
![]()
После решения имеем ![]() ,
, ![]() .
.
Проверка:
![]()
![]()
Система уравнений решена верно.
3.8. Строим эпюры M, Q, N (рис.8).
4.1. Осуществляем дискретизацию расчетной схемы и нагрузки (рис.9).
Формируем вектор нагрузки:
|
|
4.2. Образуем основную систему метода сил (рис.4).
4.3. Формируем матрицу податливости изгибным деформациям разрозненных элементов основной системы, которая имеет следующую структуру:
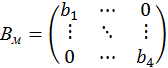
|
|
4.4. Рассмотрим единичные состояния и построим единичные эпюры m1,m2, m3 (рис.10).
4.5. Составляем матрицу влияния изгибающих моментов основной системы связанную с действием основных неизвестных:
|
|
|
|
4.4. Строим единичные эпюры связанные с нагрузкой (рис.11).
4.5. Формируем матрицу влияния основной системы связанную с влиянием действия нагрузки:
|
|
|
|
![]()
|
|
4.6. Выполняем проверку:
|
|
Проверка выполняется.
По полученным данным строим эпюру Мас (рис.12), а затем окончательную эпюру М (рис.13).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.