Составление системы уравнений для нахождения значений функции напряжений во внутриконтурных точках. Определение нормальных и касательных напряжений

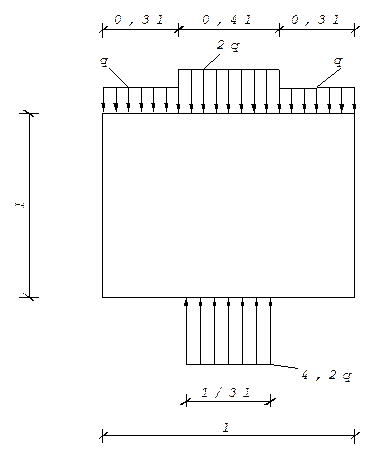
Дано:

Материал - сталь Ст;

Числовые данные:

q=1,1 кН/м

l=2,2 м.

1.Разбиваем сетку с шагом λ_x = λ_y=0,733м    

     

 

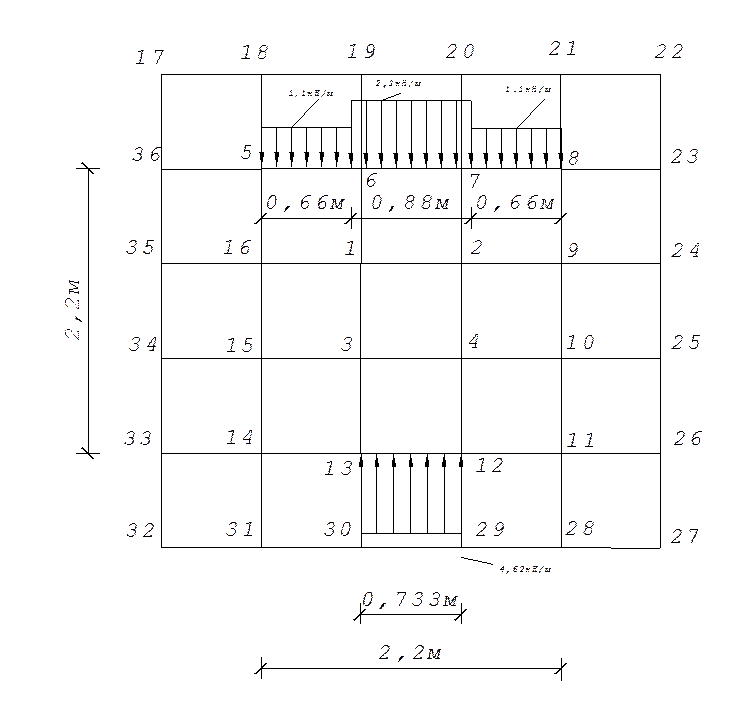
2.Рассматриваем рамный аналог и строим зпюры M,N в стержнях контура рамы:

Звено АВ:

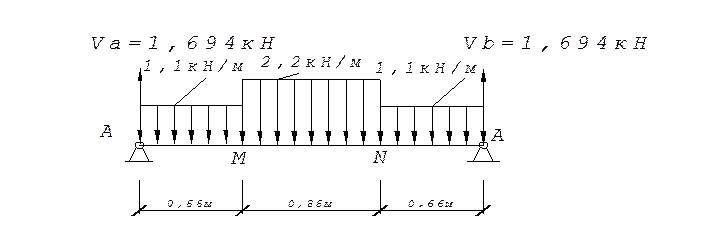
        V_A= V_B=(q*0,3l+2q*0,4l+q*0,3l)/2=0,7ql=0,7*1,1*2,2=1,694 кН;

        Проверка:

∑y=0  V_a+ V_b-1,1*0,66-2,2*0,88-1,1*0,66=0

1,694+1,694-0,726-1,936-0,726=0

Участок АМ(0≤х≤0,66):

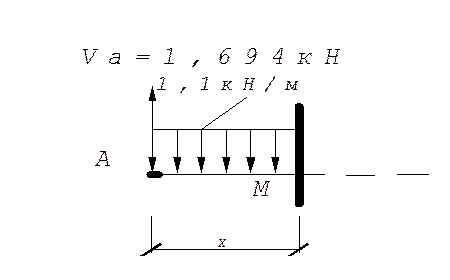
Q=1,694-1,1*х                       х=0 Q=1.694 кН;

                                                х=0,66 Q=0,968 кН;

М=-1,1*х²/2+1,694*х            х=0 M=0 кН*м;

                                                х=0,66 M=1,694*0,66-1,1*(0,66)² /2=0,878кН*м;

Участок АN(0≤х≤0,88):

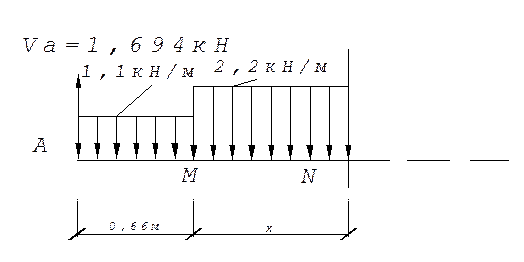
Q=1,694-1,1*0,66-2,2*х                  х=0 Q=0,968 кН;

                                                           х=0,88 Q=-0,968 кН;

 

М=-1,1*0,66*(х+0,33)+1,694*(х+0,66)-2,2*х*х/2

х=0 м                         М=0,878 кН*м;

х=0,88 м                     М=0,878 кН*м;

х_мах=0,44 м                 М=1,1 кН*м;

х=0,063 м                   М=0,94 кН*м;

х=0,796 м                   М=0,94  кН*м; _;

 

 

Участок АN(0≤х≤0,66):

 

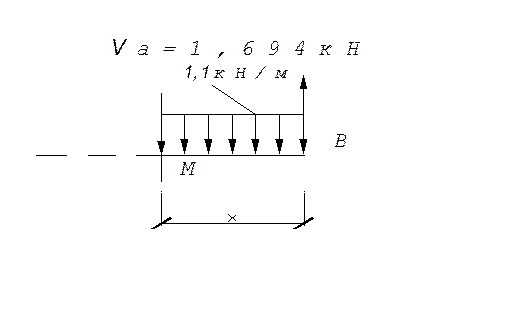
Q=-1,694+1,1*х                       х=0 Q=-1.694 кН;

                                                х=0,66 Q=-0,968 кН;

М=-1,1*х²/2+1,694*х            х=0 M=0 кН*м;

                                                х=0,66 M=1,694*0,66-1,1*(0,66)² /2=0,878кН*м;

Звено ВС:

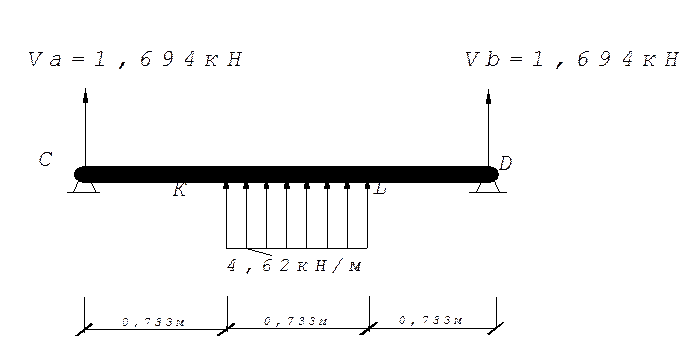
V_c= V_d=-(q*0,3l)/2=(4,62*0,733)/2=-1,694 кН;

Участок CK(0≤х≤0,733):

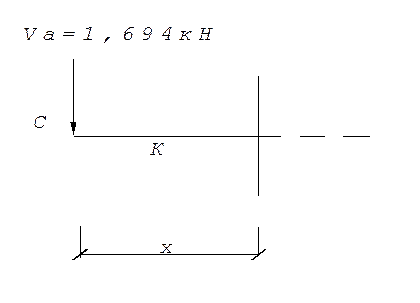
Q=-1,694кН                     

М=-1,694*х            х=0 M=0 кН*м;

                                х=0,733 M=-1,694*0,733=-1,24кН*м;

УчастоСL(0≤х≤0,733):

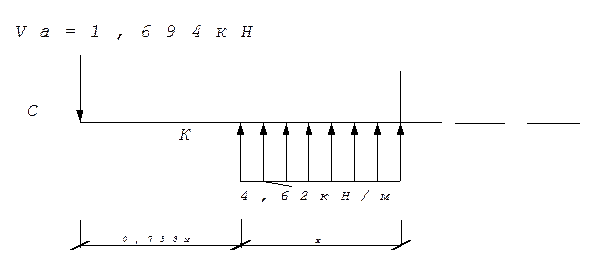
Q=-1,694+4,62*х                                       х=0 Q=1,694 кН;

                                                                    х=0,733 Q=1,694 кН;

М=-1,694*(х+0,733)+4,62*х*х/2             х=0 м                            М=-1,24 кН*м;

                                                                    х=0,733 м                     М=-1,24 кН*м;

                                                                    х_мах=0,367 м                 М=-1,55 кН*м;

УчастоLD(0≤х≤0,733):

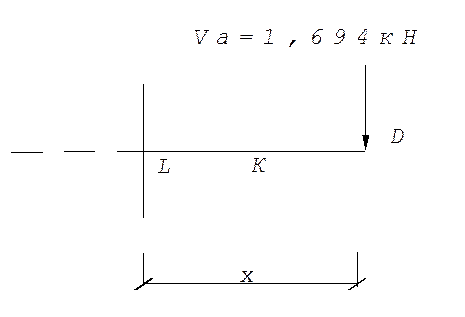
Q=1,694кН                     

М=-1,694*х            х=0 M=0 кН*м;

                                х=0,733 M=-1,694*0,733=-1,24кН*м;

                                                                                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3Определим значения функции напряжений в контурных и законтурных точках:

φ₅=0; φ₆=0,94; φ₇=0,94; φ₈=0; φ₁₄=0; φ₁₃=1,24; φ₁₂=1,24; φ₁₁=0;

φ₁₉= φ₁ + 2λ∙N₆= φ₁;

φ₃₅= φ₁ + 2λ∙N₁₆= φ₁ + 2∙0,733∙(-1,694)= φ₁ – 2,483;

φ₂₀= φ₂ + 2λ∙N₇= φ₂;

φ₂₄= φ₂ + 2λ∙N₉= φ₂ + 2∙0,733∙(-1,694)= φ₂ – 2,483;

φ₃₀= φ₃ + 2λ∙N₁₃= φ₃;

φ₃₄= φ₃ + 2λ∙N₁₄= φ₃ + 2∙0,733∙(-1,694)= φ₃ – 2,483;

φ₂₉= φ₄ + 2λ∙N₁₂= φ₄;

φ₂₅= φ₄ + 2λ∙N₁₀= φ₄ + 2∙0,733∙(-1,694)= φ₄ – 2,483;

4. Составление системы уравнений для нахождения значений функции напряжений во внутриконтурных точках

Предварительно запишем уравнения для каждой точки:

Точка1

       20·φ₁–8·(0,94+φ₂+φ₃)+2·(0,94+ φ₄)+( φ₁+1,24+ φ₁–2,483)=0

 22·φ₁–8·φ₂–8·φ₃+2·φ₄–6,883=0    

Точка2

20·φ₂–8·(0,94+φ₄+φ₁)+2·(0,94+ φ₃)+( φ₂+1,24+ φ₂–2,483)=0

–8 ·φ₁+22·φ₂+2·φ₃–8·φ₄–6,883=0   

Точка3

20·φ₃–8·(1,24+φ₄+φ₁)+2·(1,24+ φ₂)+( φ₃+0,94+ φ₃–2,483)=0

–8 ·φ₁+2·φ₂+22·φ₃–8·φ₄–8,983=0   

Точка4

20·φ₄–8·(1,24+φ₂+φ₃)+2·(1,24+ φ₁)+( φ₄+0,94+ φ₄–2,483)=0

2 ·φ₁–8·φ₂–8·φ₃+22·φ₄–8,983=0 

 

Система уравнений примет следующий вид:

22·φ₁–8·φ₂–8·φ₃+2·φ₄–6,883=0

–8 ·φ₁+22·φ₂+2·φ₃–8·φ₄–6,883=0

–8 ·φ₁+2·φ₂+22·φ₃–8·φ₄–8,983=0

2 ·φ₁–8·φ₂–8·φ₃+22·φ₄–8,983=0   

  

5. Решение системы уравнений

Матрица коэффициентов

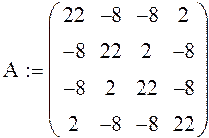
Столбец свободных членов

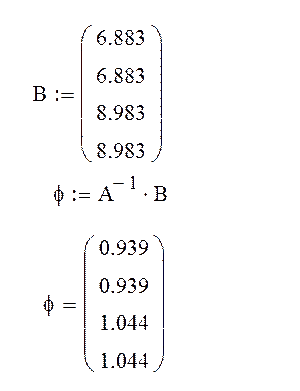
Тогда значения функции напряжений во внутриконтурных, контурных и законтурных точках будут следующими

φ₁=0,939; φ₂=0,939; φ₃=1,044; φ₄=1,044;  φ₅=0; φ₆=0,94; φ₇=0,94; φ₈=0; φ₉=0; φ₁₀=0; φ₁₁=0; φ₁₂=1,24;  φ₁₃=1,24; φ₁₄=0; φ₁₅=0; φ₁₆=0;

φ₁₈=0; φ₁₉= φ₁ + 2λ∙N₆= φ₁ =0,939; φ₂₀= φ₂ + 2λ∙N₇= φ₂=0,939; φ₂₁=0;

φ₂₃= φ₇ + 2λ∙N₈= 0,94 + 2∙0,733∙(-1,694)= – 1,543;

φ₂₄= φ₂ + 2λ∙N₉= 0,939 + 2∙0,733∙(-1,694)= – 1,544;

φ₂₅= φ₄ + 2λ∙N₁₀= 1,044 + 2∙0,733∙(-1,694)= – 1,439;

φ₂₆= φ₁₂ + 2λ∙N₁₁= 1,24 + 2∙0,733∙(-1,694)= – 1,243; φ₂₈=0;

φ₂₉= φ₄ + 2λ∙N₁₂= φ₄=1,044;

φ₃₀= φ₃ + 2λ∙N₁₃= φ₃=1,044; φ₃₁=0;

φ₃₃= φ₁₃ + 2λ∙N₁₄= 1,24 + 2∙0,733∙(-1,694)= – 1,243;

φ₃₄= φ₃ + 2λ∙N₁₄= 1,044 + 2∙0,733∙(-1,694)= -1,439;

φ₃₅= φ₁ + 2λ∙N₁₆= 0,939 + 2∙0,733∙(-1,694)= -1,544;

φ₃₆= φ₆ + 2λ∙N₅= 0,94 + 2∙0,733∙(-1,694)= – 1,543.

6. Определение нормальных и касательных напряжений

 Определение σ_X

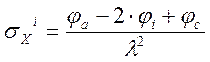
 σ_Х ⁵= σ_Х ⁸=(φ₁₈–2· φ₅+ φ₁₆)/λ²=0

σ_Х ⁶= σ_Х ⁷=(φ₁₉–2· φ₆+ φ₁)/λ²=(0,939-2·0,94+0,939)/0,733²=-0,004

σ_Х ¹⁶= σ_Х ⁹=(φ₅–2· φ₁₆+ φ₁₅)/λ²=0

σ_Х ¹= σ_Х ²=(φ₆–2· φ₁+ φ₃)/λ²=(0,94-2·0,939+1,044)/0,733²=0,197

σ_Х ¹⁵= σ_Х ¹⁰=(φ₁₆–2· φ₁₅+ φ₁₄)/λ²=0

σ_Х ³= σ_Х ⁴=(φ₁–2· φ₃+ φ₁₃)/λ²=(0,939-2·1,044+1,24)/0,733²=0,169

σ_Х ¹⁴= σ_Х ¹¹=(φ₁₅–2· φ₁₄+ φ₃₁)/λ²=0

σ_Х ¹³= σ_Х ¹²=(φ₃–2· φ₁₃+ φ₃₀)/λ²=(1,044-2·1,24+1,044)/0,733²=-0,726

 

Определение σ_Y

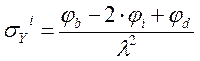
σ_Y ⁵= σ_Y ⁸=(φ₆–2· φ₅+ φ₃₆)/λ²=(0,94-2·0-1,543)/0,733²=-1,122

σ_Y ⁶= σ_Y ⁷=(φ₇–2· φ₆+ φ₅)/λ²=(0,94-2·0,94+0)/0,733²=-1,75

σ_Y ¹⁶= σ_Y ⁹=(φ₁–2· φ₁₆+ φ₃₅)/λ²=(0,939-2·0-1,544)/0,733²=-1,126

σ_Y ¹= σ_Y ²=(φ₂–2· φ₁+ φ₁₆)/λ²=(0,939-2·0,939+0)/0,733²=-1,748

σ_Y ¹⁵= σ_Y ¹⁰=(φ₃–2· φ₁₅+ φ₃₄)/λ²=(1,044-2·0-1,439)/0,733²=-0,735

σ_Y ³= σ_Y ⁴=(φ₄–2· φ₃+ φ₁₅)/λ²=(1,044-2·1,044+0)/0,733²=-1,943

σ_Y ¹⁴= σ_Y ¹¹=(φ₁₃–2· φ₁₄+ φ₃₃)/λ²=(1,24-2·0-1,243)/0,733²=-0,006

σ_Y ¹³= σ_Y ¹²=(φ₁₂–2· φ₁₃+ φ₁₄)/λ²=(1,24-2·1,24+0)/0,733²=-2,308

Определение τ_XY

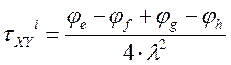
τ_ХY ¹⁶=-τ_ХY ⁹ =(φ₃₆– φ₆+ φ₃– φ₃₄)/4λ²=(-1,543-0,94+1,044+1,439)/4·0,733²=

=0

τ_ХY ¹=-τ_ХY ² =(φ₅– φ₇+ φ₄– φ₁₅)/4λ²=(0-0,94+1,044-0)/ 4·0,733² =0,048

τ_ХY ¹⁵=-τ_ХY ¹⁰ =(φ₃₅– φ₁+ φ₁₃– φ₃₃)/4λ²=(-1,544-0,939+1,24+1,243)/ 4·0,733²=

=0

τ_ХY ³=-τ_ХY ⁴ =(φ₁₆– φ₂+ φ₁₂– φ₁₄)/4λ²=(0-0,939+1,24-0)/ 4·0,733²=0,14

По полученным значениям строим эпюры σ_X , σ_Y , τ_XY

Проверка равновесия элементов балки-стенки

Составляя суммы проекций сил на оси x и y, проверим равновесие левой части балки-стенки, отсеченной по линии 6-13, и верхней части по линии 16-9 соответственно.

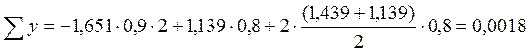
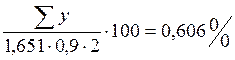
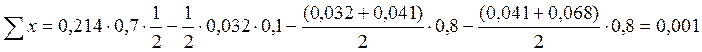
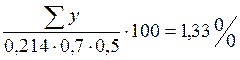
Уравнения равновесия выполняются, следовательно, решение верно.