Пример расчета плоской фермы методом сил
Исходные данные: пролет l = 24 м, высота h = 4 м, система сил P = 30 кН; жесткости: решетки EF1 = 1,5 ∙ 105 кН, верхнего пояса EF2 = 2,0 ∙ 105 кН, нижнего пояса EF3 = 3,0 ∙ 105 кН.
Расчетная схема фермы изображена на рисунке 1.
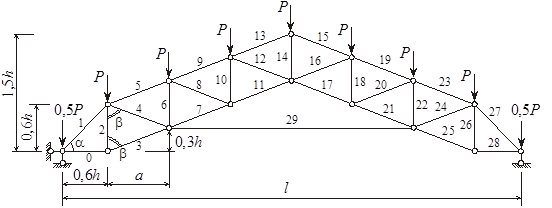
Рисунок 1
Обозначим стержни номерами 0, ..., 29. Определим величины углов α и β, а также длины стержней li (i = 0, ..., 29).
Очевидно, что α = 45˚. а = 
=
= 3,2 м; tg β
= a/(0,3h) = 3,2/(0,3 ∙
4) = 8/3, β = 69,44˚.
Длины стоек l2 = l6 = l10 = l14 = l18 = l22 = l26 = 0,6 h = 0,6 ∙ 4 = 2,4 м, стержней нижнего пояса 0 и 28 l0 = l28 = 0,6 h = 2,4 м; стержней верхнего пояса 1 и 27 l1 = l27 = 0,6 h/сos α = 0,6 ∙ 4/ cos 45˚ = 3,39 м; раскосов и остальных стержней поясов l3 = l4 = l5 = l7 = l8 = ... = 0,3 h/сos β = 0,3 ∙ 4/ cos 69,44˚ = 3,42 м; стержня 29 l29 = 4а = 4 ∙ 3,2 = 12,8 м.
Заполняем графы 1 – 3 таблицы 1, записывая номер, длину и жесткость каждого стержня.
Степень статической неопределимости вычисляем по формуле
s = – W = – (2У – С – СО),
где У – количество узлов, С – количество стержней, СО – число опорных стержней. В рассматриваемом случае У = 16, С = 30, СО = 3;
s = – (2 ∙ 16 – 30 – 3) = 1.
Ферма один раз статически неопределима.
Выбор основной системы и составление канонического уравнения
Основную систему метода сил образуем из заданной, отбрасывая одну связь (разрезая, но не устраняя лишний стержень) и вводя по ее направлению неизвестную продольную силу Х1 (рисунок 2).
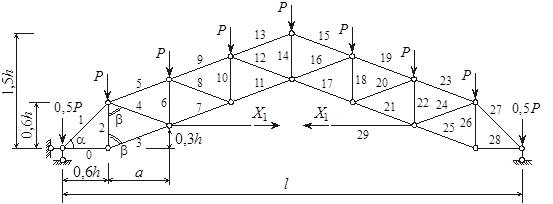
Рисунок 2
Так как ферма один раз статически неопределима, имеем одно каноническое уравнение:
δ11 Х1 + D1p = 0, (1)
где Х1 – неизвестная продольная сила в стержне 29, δ11 – единичное перемещение по направлению Х1 от действия Х1 = 1, D1p – грузовое перемещение по направлению Х1, вызванное внешней нагрузкой.
Для определения коэффициента и свободного члена уравнения (1) необходимо найти внутренние продольные силы в стержнях основной системы от действия Х1 = 1 и внешней нагрузки.
Определение усилий в стержнях основной системы от Х1 = 1. Рассматриваем единичное состояние основной системы, т. е. нагружение ее усилием Х1 = 1 (рисунок 3). Составляя уравнения моментов всех сил относительно левой и правой опор, убеждаемся, что все опорные реакции (HA, VA, VB) нулевые.
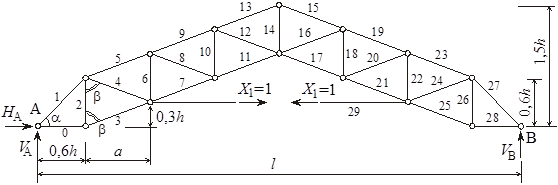
Рисунок 3
Для определения внутренних усилий воспользуемся методом вырезания узлов. Последовательно будем рассматривать равновесие узлов основной системы (рисунок 4), составляя уравнения ∑Y = 0 и ∑Z = 0.
Узел А. ΣY = 0, 
; ΣZ = 0, 
.
Узел 0-2-3.
ΣZ = 0, 
; ΣY = 0, 
.
Узел 1-2-4-5.
ΣZ = 0, 
;
ΣY = 0, 
;
.
Узел 3-4-6-7.
ΣZ = 0, 
=
– 1,068; ΣY = 0, 
=
0,375.
Узел 5-6-8-9.
ΣZ = 0, 
;
ΣY = 0, 
;
= 0,534; 
=
– 0,534.
Узел 7-8-10-11.
ΣZ = 0, 
;
= – 1,602;
ΣY = 0, 
;
= 0,375.
Узел
9-10-12-13. ΣZ = 0, 
;
ΣY = 0, 
;
= 1,068; 
=
– 0,534.
Узел 13-14-15.
ΣZ = 0, 
=
1,068; ΣY = 0, 
=
– 0,750.
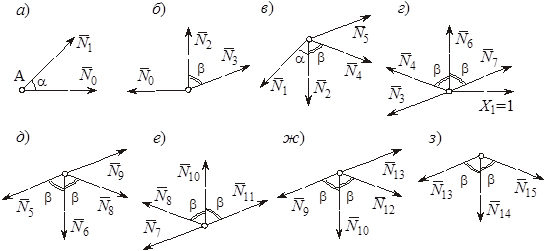
Рисунок 4
В силу симметрии основной системы и ее нагружения
= – 0,534; 
= – 1,602; 
= 0,375;
= 0,534; 
= – 0,534; 
= – 1,068;
= 0,375; 
=
=
=
=
=
=
0
Усилие в разрезанном стержне 
.
Рассчитанные значения внутренних усилий от Х1 = 1 записываем в графу 4 таблицы 1.
Определение усилий в стержнях основной системы от внешней нагрузки. Рассматриваем грузовое состояние основной системы, т. е. нагружение ее в узлах сосредоточенными силами Р (рисунок 5).
Определяем опорные реакции, рассматривая равновесие фермы в целом.
VA = VB = 0,5(7P + 2 ∙ 0,5P) = 4P = 4 ∙ 30 = 120 кН; HА = 0.
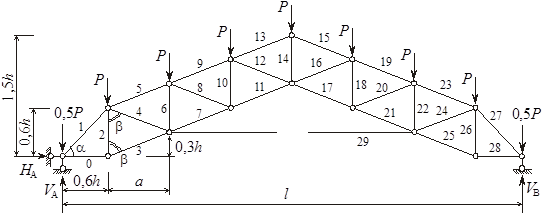
Рисунок 5
Для определения внутренних усилий воспользуемся методом вырезания узлов. Последовательно будем рассматривать равновесие узлов основной системы (рисунок 6), составляя уравнения ∑Y = 0 и ∑Z = 0.
Узел А. ΣY = 0, 
= (0,5 ∙ 30 – 4
∙ 30)/sin 45o = – 148,49 кН;
ΣZ = 0, 
= 148,49 ∙ соs 45o = 105,00 кН.
Узел 0-2-3.
ΣZ = 0, 
=
105,00 / sin 69,44о = 112,14 кН;
ΣY = 0, 
=
– 112,14 ∙ соs 69,44о = – 39,38 кН.
Узел 1-2-4-5.
ΣZ = 0, 
;
ΣY = 0, 
;
=
= 
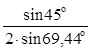(–148,49) +
=
– 218,94 кН;
= 
=
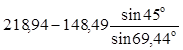106,80 кН.
Узел 3-4-6-7.
ΣZ = 0, 
;
= 112,14 + 106,80 = 218,94 кН;
ΣY = 0, 
=
(112,14 – 106,80 – 218,94)cos 69,44о =
–75,00 кН.
Узел 5-6-8-9.
ΣZ = 0, 
;
ΣY = 0, 
;
= – 218,94 + 
(30
– 75,00) = – 283,02 кН;
= 283,02 – 218,94 = 64,08 кН.
Узел 7-8-10-11.
ΣZ = 0, 
;
= 218,94 + 64,08 = 283,02 кН;
ΣY = 0, 
;
= (218,94 – 64,08 – 283,02)cos 69,44o = – 45,00 кН.
Узел
9-10-12-13. ΣZ = 0, 
;
ΣY = 0, 
;
= –283,02 + (–45,00 + 30)/(2cos 69,44о) = – 304,38 кН;
= – 283,02 + 304,38 = 21,36 кН
Узел
13-14-15. ΣZ = 0, 
=
– 304,38 кН;
ΣY = 0, 
=
– 30 + 2 ∙ 304,38 ∙ cos 69,44o = 183,75 кН.
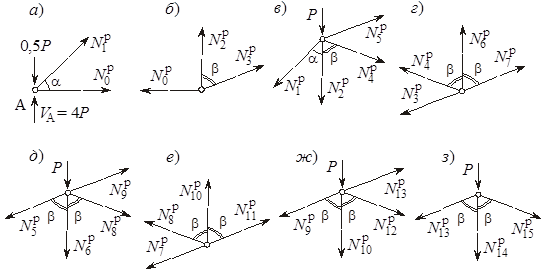
Рисунок 6
В силу симметрии основной системы и ее нагружения
= 21,36 кН; 
= 283,02 кН; 
= – 45,00 кН;
= – 283,02 кН; 
= 64,08 кН; 
= 218,94 кН;
= – 75,00 кН; 
= – 218,94 кН; 
= 106,80 кН;
= 112,14 кН; 
= – 39,38 кН; 
= – 148,49 кН;
= 105,00 кН. Усилие
в разрезанном стержне 
.
Рассчитанные значения внутренних усилий от внешней нагрузки записываем в графу 5 таблицы 1.
Определение единичного и грузового перемещений. Решение канонического уравнения. Коэффициент (единичное перемещение) и свободный член (грузовое перемещение) канонического уравнения (1) вычисляем по формулам:
δ11
= ∑
; D1p = ∑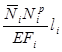
.
Здесь li, EFi – длина
и жесткость i-го
стержня, 
, 
–
усилия в нем от Х1 = 1 и от внешней нагрузки (i = 0, ..., 29).
Для каждого стержня вычисляем величины и
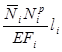, заносим их соответственно в графы 6
и 7 таблицы 1, затем проводим суммирование по всем стержням. Значения
полученных сумм записываем в последнюю строку таблицы. Это и есть искомые δ11
и D1p
:
δ11 = 219,84 ∙ 10–6 м/кН; D1p = – 376,57 ∙ 10–4 м.
Далее из уравнения (1) определяем продольную силу в стержне 29:
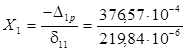= 171,3 кН.
Вычисление окончательных значений продольных сил. Находим усилия в стержнях основной системы от действительного значения Х1, умножая данные графы 4 на Х1 = 171,3 кН. Результат записываем в графу 8.
Определяем окончательные продольные усилия в стержнях фермы:
,
где Ni – усилие в i-ом стержне заданной статически неопределимой фермы от внешней нагрузки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
