Исходные данные. Пролет l = 30 м, стрела подъема f = 6,2 м, очертание оси – квадратная парабола
![]() ,
,
начало координат – на левой опоре; вертикальные внешние нагрузки: q = 5 кН/м, P = 45 кН, жесткости EJ = 1,5 ∙ 106 кН ∙ м2, EF = 2,5 ∙ 107 кН.
Расчетная схема арки изображена на рисунке 1.
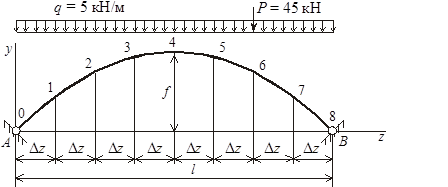
Рисунок 1
Геометрические параметры оси арки. Разобьем пролет арки на 8 равных
частей так, чтобы сосредоточенная сила совмещалась с точкой деления, примем Δz = l/8 = 30/8 = 3,75 м,
выберем 9 расчетных сечений на оси (0, …, 8). Положение k-го
сечения характеризуется тремя параметрами: абсциссой zk
= kΔz, ординатой ![]() и углом наклона касательной к оси
арки jk.
и углом наклона касательной к оси
арки jk.
Для вычисления jk продифференцируем функцию ![]() :
:
![]() . Отсюда
. Отсюда ![]() .
Вычисляем также значения sin jk и cos jk.
.
Вычисляем также значения sin jk и cos jk.
Рассчитанные параметры арки записываем в графы 1–6 таблицы 1.
Выбор основной системы и составление канонического уравнения. Арка один раз статически неопределима. Для ее расчета методом сил выбираем балочную основную систему, т. е. представляем арку в виде статически определимой криволинейной балки на двух опорах. Для этого отбрасываем в точке В горизонтальный опорный стержень и вводим неизвестную силу Х1 (рисунок 2).
Каноническое уравнение запишется следующим образом:
![]() ,
,
где Х1 – неизвестная горизонтальная сила, δ11 – единичное перемещение по направлению Х1 от действия Х1 = 1, D1p – грузовое перемещение по направлению Х1, вызванное внешней нагрузкой.
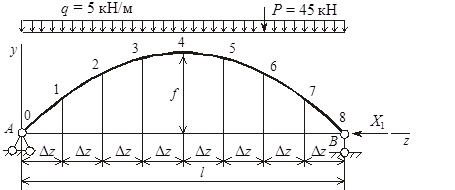
Рисунок 2
Для определения коэффициента и свободного члена канонического уравнения необходимо найти внутренние усилия в основной системе от действия Х1 = 1 и внешней нагрузки.
Определение усилий в основной системе от Х1 = 1. Рассматриваем единичное состояние основной системы, т. е. нагружение ее усилием Х1 = 1 (рисунок 3). Составляя уравнения моментов всех сил относительно левой и правой опор, убеждаемся, что вертикальные опорные реакции нулевые, а горизонтальная реакция левой опоры равна 1.
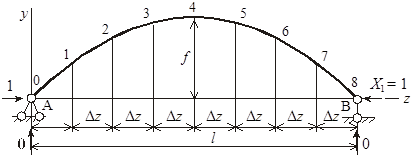
Рисунок 3
Изгибающие моменты, поперечные и продольные силы в основной системе от Х1 = 1 определяем по формулам:
![]() ;
; ![]() ;
;
![]() .
.
Рассчитываем внутренние усилия в сечениях 0, ..., 8 и записываем их в графы 7–9 таблицы 1.
Определение усилий в основной системе от внешней нагрузки. Рассматриваем грузовое состояние основной системы, т. е. воздействие на нее вертикальных нагрузок q и Р (рисунок 4).
Для исследуемой арки будут справедливы формулы по расчету внутренних усилий в трехшарнирной арке. Очевидно, что распор НА = 0.
Вначале определим опорные реакции и внутренние усилия в соответствующей балке (рисунок 5).
Опорные реакции балки VAб, VBб вычислим из уравнений статики:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
отсюда ![]() кН,
кН,
![]() кН.
кН.
Проверка: ![]() ,
,
![]() .
.
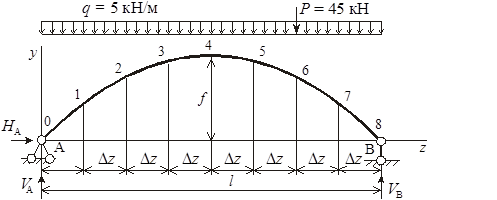
Рисунок 4
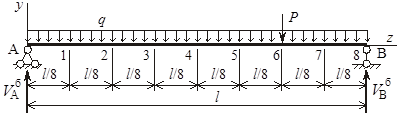
Рисунок 5
Вычисляем внутренние поперечные силы Qрб и изгибающие моменты Мрб в сечениях балки 0, …, 8.
Qр0б = VAб = 86 кН, Мр0б = 0;
Qр1б = VAб – qz1 = 86 – 5 × 3,75 = 67,3 кН,
Мр1б = VAбz1 – qz12/2 = 86 × 3,75 – 5 × 3,752/2 = 287,3 кН × м;
Qр2б = VAб – qz2 = 86 – 5 × 7,5 = 48,5 кН,
Мр2б = VAбz2 – qz22/2 = 86 × 7,5 – 5 × 7,52/2 = 504,4 кН × м;
Qр3б = VАб – q z3 = 86 – 5 × 11,25 = 29,8 кН,
Мр3б = VАб z3 – q z32/2 = 86 × 11,25 – 5 × 11,252/2 = 651,1 кН × м;
Qр4б = VАб – q z4 = 86 – 5 × 15 = 11 кН,
Мр4б = VАб z4 – q z42/2 = 86 × 15 – 5 × 152/2 = 727,5 кН × м;
Qр5б = VАб – q z5 = 86 – 5 × 18,75 = – 7,8 кН,
Мр5б = VАб z5 – q z52/2 = 86 × 18,75 – 5 × 18,752/2 = 733,6 кН × м;
Qр6б лев = VАб – q z6 = 86 – 5 × 22,5 = – 26,5 кН (левее силы Р), Qр6б прав = VAб – qz6 – Р = 86 – 5 × 22,5 – 45 = – 71,5 кН (правее силы Р), Мр6б = VАб z6 – q z62/2 = 86 × 22,5 – 5 × 22,52/2 = 669,4 кН × м;
Qр7б = – VВб + q(l – z7) = – 109 + 5 × 3,75 = – 90,3 кН,
Мр7б = VBб(l – z7) – q(l – z7)2/2 = 109 × 3,75 – 5 × 3,752/2 = 373,6 кН × м;
Qр8б = – VВб = – 109 кН, Мр8б = 0.
Рассчитанные значения заносим в графы 10 и 11 таблицы 1.
Вертикальные составляющие опорных реакций основной системы VA и VB равны опорным реакциям соответствующей балки
![]() кН,
кН, ![]() кН.
кН.
Внутренние усилия в основной системе от внешней нагрузки рассчитываем по формулам:
а) изгибающий момент ![]() ;
;
б) поперечная сила ![]() ;
;
в) продольная сила ![]() .
.
Значения внутренних усилий от внешней нагрузки записываем в графы 12–14 таблицы 1.
Таблица 1.
|
№ сечения |
Геометрические параметры оси арки |
Усилия в о. с. от Х1 = 1 |
Усилия от внешней нагрузки |
|||||||||||
|
(q = 5 кН/м, Р = 45 кН) |
||||||||||||||
|
в соответствующей балке |
в основной системе |
|||||||||||||
|
z, м |
y, м |
j, рад |
sin j |
cos j |
__ М1 = – y, м |
__ Q1 = – sin j |
__ N1 = – cos j |
Mpб , кН × м |
Qpб , кН |
Mp = Mpб, кН × м |
Qp = Qpб cos j, кН |
Np = – Qpб sin j , кН |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
0 |
0,000 |
0,000 |
0,691 |
0,637 |
0,771 |
0,000 |
-0,637 |
-0,771 |
0,000 |
86,000 |
0,000 |
66,284 |
-54,795 |
|
|
1 |
3,750 |
2,713 |
0,555 |
0,527 |
0,850 |
-2,713 |
-0,527 |
-0,850 |
287,300 |
67,300 |
287,300 |
57,198 |
-35,463 |
|
|
2 |
7,500 |
4,650 |
0,392 |
0,382 |
0,924 |
-4,650 |
-0,382 |
-0,924 |
504,400 |
48,500 |
504,400 |
44,822 |
-18,526 |
|
|
3 |
11,250 |
5,813 |
0,204 |
0,202 |
0,979 |
-5,813 |
-0,202 |
-0,979 |
651,100 |
29,800 |
651,100 |
29,183 |
-6,031 |
|
|
4 |
15,000 |
6,200 |
0,000 |
0,000 |
1,000 |
-6,200 |
0,000 |
-1,000 |
727,500 |
11,000 |
727,500 |
11,000 |
0,000 |
|
|
5 |
18,750 |
5,813 |
-0,204 |
-0,202 |
0,979 |
-5,813 |
0,202 |
-0,979 |
733,600 |
-7,800 |
733,600 |
-7,639 |
-1,579 |
|
|
6 (слева) |
22,500 |
4,650 |
-0,392 |
-0,382 |
0,924 |
-4,650 |
0,382 |
-0,924 |
669,400 |
-26,500 |
669,400 |
-24,490 |
-10,123 |
|
|
6 (справа) |
22,500 |
4,650 |
-0,392 |
-0,382 |
0,924 |
-4,650 |
0,382 |
-0,924 |
669,400 |
-71,500 |
669,400 |
-66,078 |
-27,312 |
|
|
7 |
26,250 |
2,713 |
-0,555 |
-0,527 |
0,850 |
-2,713 |
0,527 |
-0,850 |
373,600 |
-90,300 |
373,600 |
-76,746 |
-47,583 |
|
|
8 |
30,000 |
0,000 |
-0,691 |
-0,637 |
0,771 |
0,000 |
0,637 |
-0,771 |
0,000 |
-109,000 |
0,000 |
-84,011 |
-69,449 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.