Расчёт двухшарнирной арки методом сил, страница 2

Определение единичного и грузового перемещений. Решение канонического уравнения. Коэффициент (единичное перемещение) и свободный член (грузовое перемещение) канонического уравнения  вычисляем по формулам:

,   .

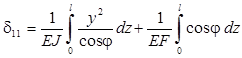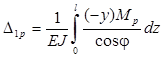При расчете используем формулу трапеций приближенного численного интегрирования. Для этого в каждом из сечений 0, ..., 8 вычисляем значения подынтегральных функций (графы 2, 5, 8 таблицы 2) и указываем соответствующие формуле трапеций множители (графы 3, 6, 9). Далее заполняем графы 4, 7, 10 таблицы 2, умножая значение функции в расчетном сечении на множитель. После этого проводим суммирование полученных чисел по всем расчетным сечениям, результат записываем в последней строке таблицы 2 (Σ₁, Σ₂, Σ₃).

Чтобы получить искомые интегралы, необходимо суммы Σ₁, Σ₂, Σ₃ умножить на Δz/2:

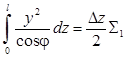 =  = 643,298 м³,  

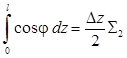 =  = 27,291 м,  

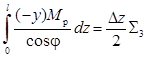 =  = – 77792 кН ∙ м³.

Таблица 2

№ сечения	Расчет единичного перемещения						Расчет грузового			Усилия в о.с. от действительного                Х1 = 120,6 кН			Окончательные усилия в заданной системе
							перемещения
	1-е слагаемое			2-е слагаемое				Множитель		кН ∙ м	кН	кН	M,            кН ∙ м	Q,               кН	N,               кН
		Множитель		cos φ	Множитель
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
0	0,000	1	0,000	0,771	1	0,771	0,000	1	0,000	0,000	-76,840	-92,952	0,000	-10,556	-147,746
1	8,657	2	17,314	0,850	2	1,700	-916,930	2	-1833,860	-327,128	-63,549	-102,498	-39,828	-6,350	-137,961
2	23,397	2	46,793	0,924	2	1,848	-2537,918	2	-5075,837	-560,790	-46,068	-111,455	-56,390	-1,246	-129,981
3	34,499	2	68,998	0,979	2	1,959	-3864,494	2	-7728,988	-700,988	-24,408	-118,104	-49,887	4,775	-124,135
4	38,440	2	76,880	1,000	2	2,000	-4510,500	2	-9021,000	-747,720	0,000	-120,600	-20,220	11,000	-120,600
5	34,499	2	68,998	0,979	2	1,959	-4354,159	2	-8708,318	-700,988	24,408	-118,104	32,613	16,770	-119,683
6(слева)	23,397	2	46,793	0,924	2	1,848	-3368,125	2	-6736,251	-560,790	46,068	-111,455	108,610	21,577	-121,577
6(справа)										-560,790	46,068	-111,455	108,610	-20,010	-138,767
7	8,657	2	17,314	0,850	2	1,700	-1192,360	2	-2384,720	-327,128	63,549	-102,498	46,473	-13,197	-150,081
8	0,000	1	0,000	0,771	1	0,771	0,000	1	0,000	0,000	76,840	-92,952	0,000	-7,171	-162,401
Σ1		343,092		Σ2	14,555		Σ3	-41488,974

Вычисляем  единичное и грузовое перемещения:

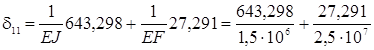 = 4,3 ∙ 10^–3 ,

 = – 518,6 ∙ 10^–3 м.

Далее из уравнения (2.1) определяем неизвестную силу:

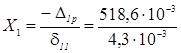 = 120,6 кН.

Вычисление окончательных значений внутренних усилий. Находим усилия в основной системе от действительного значения  Х₁, умножая данные граф 7, 8, 9 таблицы 1  на  Х₁ = 120,6 кН.  Результаты записываем в графы 11, 12, 13 таблицы 2.

Окончательные изгибающие моменты, поперечные и продольные силы в арке определяем по формулам:

,  ,  .

Для каждого из расчетных сечений 0, ..., 8 вычисляем значения внутренних усилий, используя данные граф 11–13 таблицы 2  и  12–14 таблицы 1. Результат записываем в графы 14, 15, 16 таблицы 2. По полученным данным строим эпюры M, Q, N (рисунок 6).

Деформационная проверка. Вычисляем суммарное перемещение

.

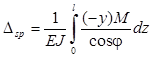Если расчет выполнен верно, оно должно получиться нулевым.

Расчет ведем в табличной форме (таблица 3). Искомое суммарное перемещение находим аналогично грузовому перемещению D_1p, используя формулу трапеций:

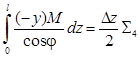 =  = – 210,27 кН ∙ м³.

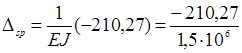 = 0,001 м 0.

Точность подсчетов приемлемая. Значение  D_sp  близко к нулю, следовательно, моменты в арке найдены верно.

            Таблица 3

№ сечения	y, м	M,  кН ∙ м	cos φ	Расчет перемещения
					Множи-тель
0	0,000	0,000	0,771	0,000	1	0,000
1	2,713	-39,828	0,850	127,122	2	254,243
2	4,650	-56,390	0,924	283,781	2	567,562
3	5,813	-49,887	0,979	296,214	2	592,427
4	6,200	-20,220	1,000	125,364	2	250,728
5	5,813	32,613	0,979	-193,646	2	-387,292
6	4,650	108,610	0,924	-546,576	2	-1093,153
7	2,713	46,473	0,850	-148,331	2	-296,662
8	0,000	0,000	0,771	0,000	1	0,000
Σ4					-112,146

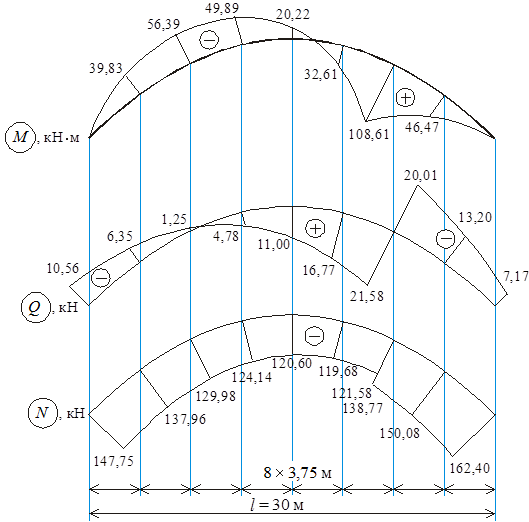
Рисунок 6