Математика \ Высшая математика

Определенный интеграл и его приложения

Страницы работы

31 страница (Word-файл)

Скачать файл

Содержание работы

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Кафедра высшей математики

Определенный интеграл

и его приложения

Методические указания и контрольные задания для студентов первых курсов всех специальностей очной формы обучения

Составители: Гуменникова Ю.В.,

Лаврусь О.Е.,

Хайруллина Р.Н.

Самара 2008

УДК 519.7

Высшая математика: Методические указания и контрольные задания для студентов первых курсов всех специальностей очной формы обучения / Ю.В. Гуменникова, О.Е. Лаврусь, Р.Н. Хайруллина; Самара: СамГУПС, 2008. 60 с.

Утверждено на заседании кафедры протокол № 7 от 09.06.2008.

Печатается по решению редакционно-издательского совета университета

Методические указания составлены в соответствии с Государственным образовательным стандартом, с действующей программой по высшей математике для технических специальностей и охватывают все методы вычисления неопределенного интеграла.

В методических указаниях приведены индивидуальные задания, необходимые теоретические сведения, а также примеры решения задач.

Предназначены для студентов 1-ого курса всех специальностей очной формы обучения.

Составители: Ю.В. Гуменникова, к.ф.-м.н., доцент,

О.Е. Лаврусь, к.т.н., доцент,

Р.Н. Хайруллина, преподаватель

Рецензенты: к. ф.-м. н., доцент кафедры «Высшая математика»

СГАУ О.А. Васильева к. ф.-м. н., доцент кафедры «Высшая математика»

СамГУПС Л.В. Кайдалова

Под редакцией зав. кафедрой «Высшая математика» Кузнецова В.П.

Редактор: ___________

Компьютерная верстка:

Подписано в печать ________ Формат 60х84. 1/16

Бумага писчая. Печать оперативная. Усл.п.л.

Тираж 500 экз. Заказ № __

ÓСамарский государственный университет путей сообщения, 2008

Содержание

Определённый интеграл §1. Вычисление определённого интеграла…………………………………………….	4
Задание 1. ……………………………………………………………………………….	7
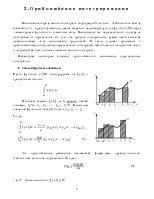
§2. Приближенное интегрирование……………………………………………………	12
Задание 2. ………………………………………………………………………………..	16
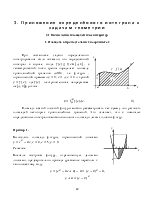
§3. Приложение определенного интеграла к задачам геометрии 3.1 Вычисление площадей плоских фигур 1. Площадь в прямоугольных координатах…………………………………	18
2. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме………………………………………………………	21
3. Площадь криволинейного сектора………………………………………..	22
Задание 3………………………………………………………………………………….	23
Задание 4………………………………………………………………………………….	26
Задание 5………………………………………………………………………………….	27
3.2 Вычисление длины дуги плоской кривой……………………………………	28
Задание 6………………………………………………………………………………….	30
Задание 7………………………………………………………………………………….	32
Задание 8………………………………………………………………………………….	33
3.3 Вычисление объёмов тел 1. Объём тела с заданным поперечным сечением…………………………..	34
2. Объём тела вращения………………..…………………………………….	36
Задание 9………………………………………………………………………………….	38
Задание 10………………………………………………………………………………...	40
Задание 11………………………………………………………………………………...	41
3.4. Вычисление площади поверхности вращения……………………………...	43
Задание 12………………………………………………………………………………..	45
§4. Приложения определённого интеграла к решению некоторых задач физического содержания 4.1. Вычисление пройденного пути по скорости……………………………….	46
4.2. Вычисление работы переменной силы……………………………………..	47
4.3. Вычисление силы давления жидкости на пластину……………………….	48
4.4. Вычисление координат центра масс плоской фигуры…………………….	49
Задание 13………………………………………………………………………………..	50
Задание 14………………………………………………………………………………..	51
Задание 15………………………………………………………………………………..	54
§5. Несобственные интегралы 5.1. Основные понятия……………………………………………………………	55
5.2. Признаки сравнения…………………………………………………………..	56
Задание 16………………………………………………………………………………...	57

Определённый интеграл

1. Вычисление определённого интеграла

Пусть функция f(x) определена на отрезке . Разделим отрезок на n произвольных частей точками a=x₀<x₁<x₂<…<<=b, выберем на каждом элементарном отрезке произвольную точку ξ и найдём длину каждого такого отрезка ∆ =.

Интегральной суммой для функции f(x) на отрезке называется сумма вида σ= причём эта сумма имеет конечный предел I, если для каждого ε>0 найдётся такое число δ>0, что при max неравенство выполняется при любом выборе чисел .

Определённым интегралом от функции f(x) на отрезке (или в пределах от ) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков (max ) стремится к нулю: