![]() = 8π
= 8π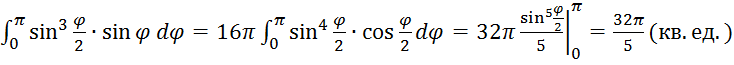 .
.
4. Приложения определённого интеграла к решению некоторых задач физического содержания
4.1. Вычисление пройденного пути по скорости
Пусть ![]() - скорость движения материальной
точки по прямой. Тогда путь S,
пройденный этой точкой за время t
(t
- скорость движения материальной
точки по прямой. Тогда путь S,
пройденный этой точкой за время t
(t![]() ), вычисляется по формуле
), вычисляется по формуле
![]() (1)
(1)
Пример 1.
Некоторое
тело движется прямолинейно со скоростью ![]()
![]() . Найти путь, пройденный телом за 3
секунды после начала движения.
. Найти путь, пройденный телом за 3
секунды после начала движения.
Решение.
По формуле (1) имеем:
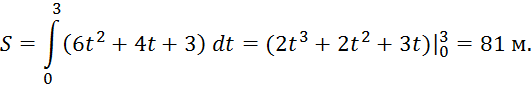
4.2. Вычисление работы переменной силы
Пусть некоторое тело движется по прямой l
под действием переменной силы ![]() . Работа этой силы на участке пути
. Работа этой силы на участке пути ![]() вычисляется по формуле
вычисляется по формуле
![]() (2)
(2)
Пример 2.
Вычислить работу, которую необходимо затратить, чтобы растянуть пружину на 20 см, если известно, что для удлинения её на 1 см нужно приложить силу в 1 кН.
Решение:
Согласно закону Гука, сила ![]() растяжения
пружины пропорциональна её растяжению, т.е.
растяжения
пружины пропорциональна её растяжению, т.е. ![]() где
где ![]() растяжение пружины (в метрах),
растяжение пружины (в метрах), ![]() коэффициент пропорциональности.
коэффициент пропорциональности.
Т.к. по условию при ![]() м сила
м сила ![]() , то из равенства
, то из равенства ![]() получаем
получаем ![]() . Следовательно, искомая работа
. Следовательно, искомая работа
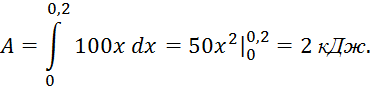
4.3. Вычисление силы давления жидкости на пластину
Решение данной задачи покажем на примере.
 Пример
3.
Пример
3.
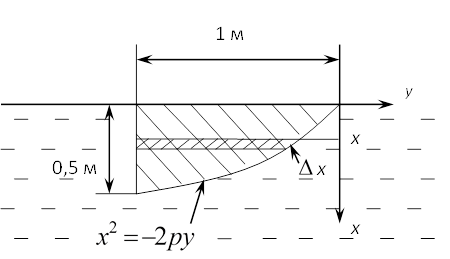
Вычислить силу давления воды на пластину,
вертикально погруженную в воду, считая что удельный вес воды равен 9,81 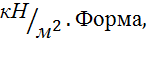 размеры и расположение пластины
указаны на рисунке.
размеры и расположение пластины
указаны на рисунке.
Решение.
Задаём систему координат относительно пластины.
Простейшее
уравнение параболы в данном случае имеет вид ![]() Т.к. парабола проходит через т.
А(0,5;-1), то находим p:
Т.к. парабола проходит через т.
А(0,5;-1), то находим p:
![]() т.е. уравнение параболы
т.е. уравнение параболы
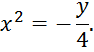
Выделим
на глубине ![]() горизонтальную полоску шириной
горизонтальную полоску шириной ![]() и площадью
и площадью ![]() . Давление воды на эту полоску
. Давление воды на эту полоску
![]()
Тогда давление воды на всю пластину
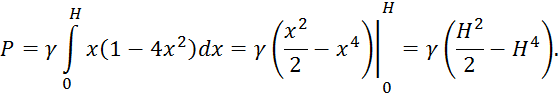
При
Н=0,5м и ![]() =9,81
=9,81 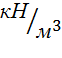 получаем:
получаем:
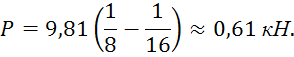
4.4. Вычисление координат центра масс плоской фигуры
1.
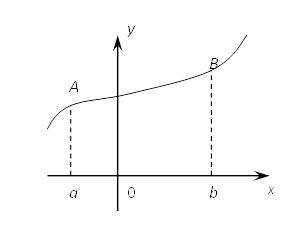 Координаты центра масс плоской линии.
Координаты центра масс плоской линии.
Рассмотрим дугу АВ графика функции ![]() имеющую линейную плотность
имеющую линейную плотность ![]() Координаты центра масс С(xc,
yc) такой дуги вычисляются
по формулам:
Координаты центра масс С(xc,
yc) такой дуги вычисляются
по формулам:
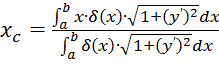 ,
,
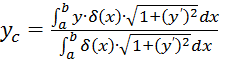 (4)
(4)
2. Координаты центра масс плоской фигуры.
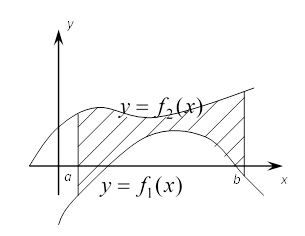 Рассмотрим фигуру, ограниченную снизу линией
Рассмотрим фигуру, ограниченную снизу линией ![]() сверху -
сверху - ![]() т.е.
т.е. ![]() на отрезке
на отрезке ![]() поверхностная плотность фигуры
поверхностная плотность фигуры ![]() Центр масс такой фигуры
Центр масс такой фигуры ![]() вычисляется по формулам
вычисляется по формулам
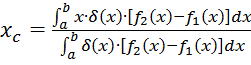 ,
,
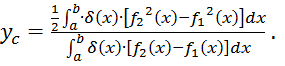
![]()
 Пример
4.
Пример
4.
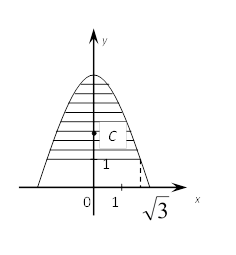
Найти
координаты центра масс однородной фигуры, ограниченной линиями ![]()
Решение.
Из
симметричности и однородности этой фигуры очевидно, что ![]() Определим
Определим ![]() по формуле
по формуле ![]()
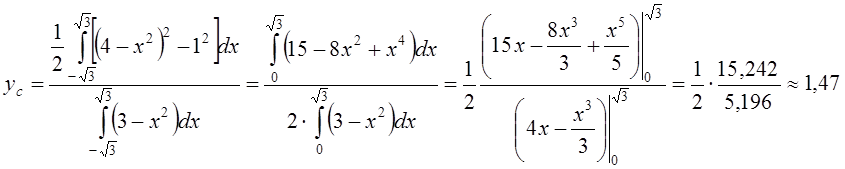 .
.
5. Несобственные интегралы
5.1. Основные понятия
Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций.
Несобственный интеграл от функции ![]() от
от ![]() определяется равенством
определяется равенством 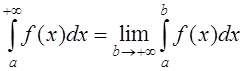 . Если этот предел
существует и конечен, то несобственный интеграл называется сходящимся;
если же этот предел не существует или равен бесконечности, - расходящимся.
Аналогично:
. Если этот предел
существует и конечен, то несобственный интеграл называется сходящимся;
если же этот предел не существует или равен бесконечности, - расходящимся.
Аналогично: 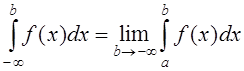 и
и
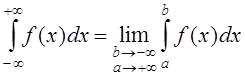 .
.
Если функция ![]() имеет бесконечный разрыв в точке С
отрезка
имеет бесконечный разрыв в точке С
отрезка ![]() и непрерывна при
и непрерывна при ![]() , то по определению полагают
, то по определению полагают
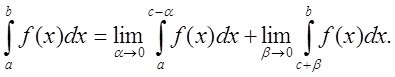
Несобственный интеграл ![]() (где
(где ![]() ) называется сходящимся если
существуют оба предела в правой части равенства, и расходящимся, если не
существует хотя бы один из них.
) называется сходящимся если
существуют оба предела в правой части равенства, и расходящимся, если не
существует хотя бы один из них.
Пример 1.
Найти несобственный интеграл (или установить его расходимость)
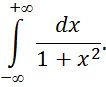
Решение: т.к. подынтегральная функция чётная, то
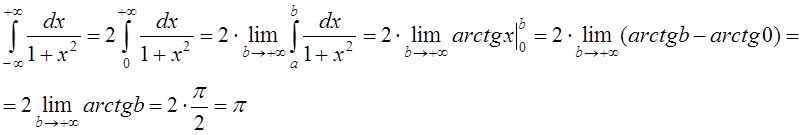
таким
образом, 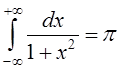 ,
поэтому несобственный интеграл сходится.
,
поэтому несобственный интеграл сходится.
Пример 2.
Найти:
![]() (или установить его расходимость).
(или установить его расходимость).
Решение: Подынтегральная функция при х=0 не существует, т.е. неограниченна, поэтому запишем
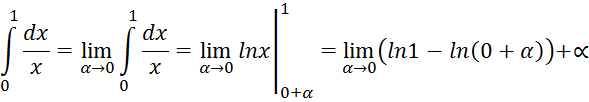
т.е. несобственный интеграл расходится
5.2 Признаки сравнения
При исследовании сходимости несобственных интегралов пользуются одним из признаков сравнения.
1) Если
функции ![]() определены для всех
определены для всех ![]() и интегрируемы на отрезке
и интегрируемы на отрезке ![]() , где
, где ![]() , и если
, и если ![]() для всех
для всех ![]() , то из сходимости интеграла
, то из сходимости интеграла ![]() вытекает сходимость интеграла
вытекает сходимость интеграла
![]() причём
причём ![]()
2) а)
Если при ![]() функция
функция ![]() является бесконечно малой порядка
является бесконечно малой порядка ![]() то интеграл
то интеграл ![]() сходится при
сходится при ![]() и расходится при
и расходится при ![]()
б) Если функция ![]() определена и непрерывна в
промежутке
определена и непрерывна в
промежутке ![]() и является бесконечно большой
порядка p по сравнению с
и является бесконечно большой
порядка p по сравнению с ![]() при
при ![]() то интеграл
то интеграл ![]() сходится при
сходится при ![]() и расходится при
и расходится при![]()
Пример.
Исследовать сходимость интеграла
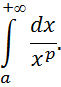
Решение. По определению
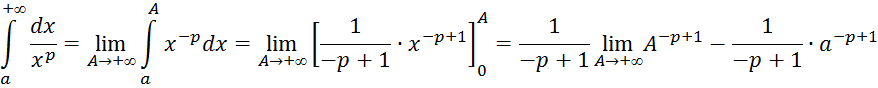
Допустим,
что ![]() , тогда
, тогда ![]() , значит интеграл сходится.
, значит интеграл сходится.
Пусть
![]() тогда
тогда ![]() тогда интеграл расходится.
тогда интеграл расходится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.