Определенный интеграл и его приложения, страница 4

Находим абсциссы точек пересечения прямой  с параболами  и  Прямой  разобьём данную фигуру на две части – ОАСО и САВС. Площадь S данной фигуры равна сумме площадей этих частей:

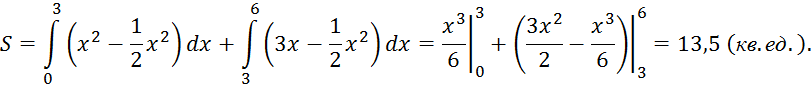
2. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме

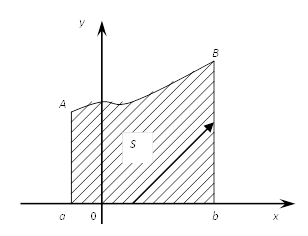Если кривая АВ, ограничивающая криволинейную трапецию  задана параметрическими уравнениями

 

То площадь криволинейной трапеции вычисляется по формуле:

                                            (4′)

Кроме того функции  должны удовлетворять следующим условиям:

1)   непрерывна и неотрицательна на

2)    имеет непрерывную производную на

3)   знакопостоянна на  или  если  и  если

Пример 5.

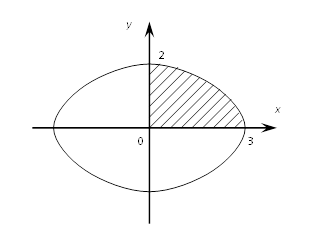Вычислить площадь фигуры, ограниченной эллипсом

Решение.

Запишем параметрические уравнения эллипса:

Учитывая свойства симметрии фигуры и формулу (4) получаем

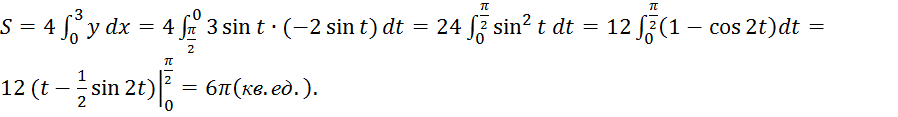
Заметим, что пределы интегрирования  были найдены по формулам (4′):

 

 

3. Площадь криволинейного сектора

Иногда кривая может быть задана не в прямоугольной системе координат, а в полярной, уравнением

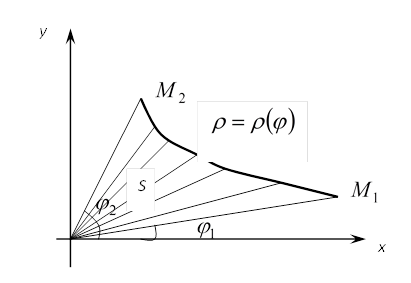
Площадь криволинейного сектора OM₁M₂, ограниченного дугой такой кривой и двумя полярными радиусами OM₁ и OM₂, соответствующими значениям 𝜑₁ и 𝜑₂ полярного угла, вычисляется по формуле:

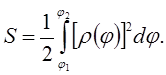                                                             (5)

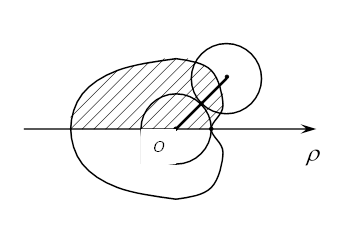
Пример 6. Найти площадь кардиоиды

Решение. Кардиоида  это кривая, описываемая произвольной точкой окружности круга диаметром a, катящейся без трения и скольжения по неподвижной окружности того же диаметра. Из соображений симметрии и по формуле (5) получаем:

 

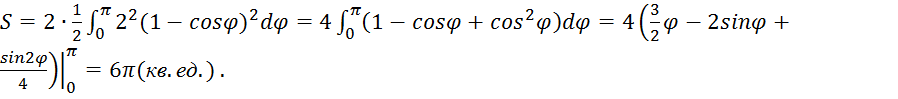
3.2 Вычисление длины дуги плоской кривой

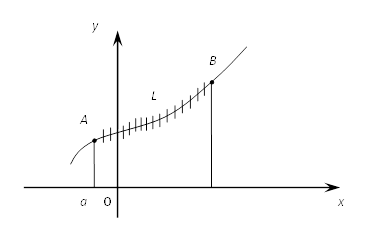1. Длина дуги кривой, заданной в прямоугольных координатах.

Пусть дуга  АВ плоской кривой задана уравнением y=f(x), где f(x) – непрерывно дифференцируемая функция. Тогда длина дуги АВ определяется по формуле

                                              (6)

Пример 6.

Вычислить длину дуги кривой , абсциссы концов которой  х=1,  х=4.

Решение.

Т.к.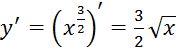, согласно формуле (6) имеем:

.

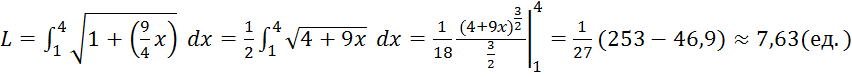В случае, когда кривая задана параметрическими уравнениями x=(t), y=ψ(t), где (t), ψ(t) – непрерывно дифференцируемые функции, длина дуги  вычисляется по формуле:

                                       (7), где  и  – значение параметра  соответствующие концам дуги А и В, т.е.

(t₀) = a, (T) = b.

Пример 7.

Вычислить длину дуги одной арки циклоиды , x=3(tsin t).

Решение.

Т.к. все арки циклоиды равны, рассмотрим первую ее арку, вдоль которой параметр t меняется от 0 до 2π.

Согласно формуле (7) имеем

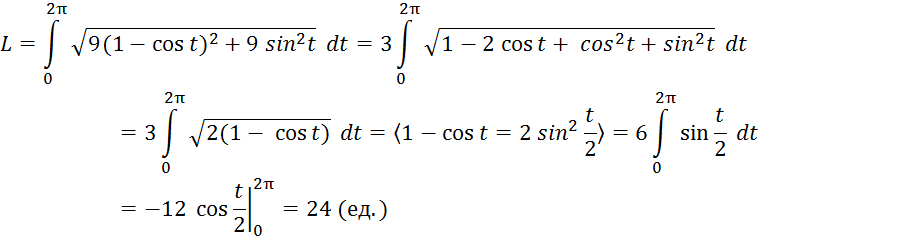
Если кривая задана в полярных координатах уравнением , то длина дуги М₁М₂ вычисляется по формуле

                                       (8)

где и  соответствует концам дуги М₁ и М₂.

Пример 8.

Вычислить длину кардиоиды .

Решение. Находим

 

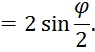
Т.к. кардиоида симметрична относительно полярной оси, то найдём длину половины этой линии , изменяя полярный угол от 0 до π, а затем удвоим результат. По формуле (8) получаем

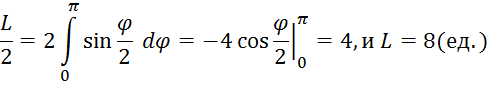
3.3 Вычисление объёмов тел

1. Объём тела с заданным поперечным сечением

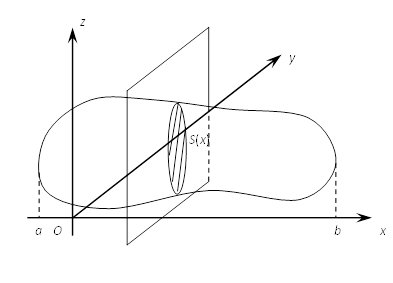Пусть в системе координат OXYZ имеется тело, ограниченное замкнутой поверхностью. Пересечём данное тело плоскостью, перпендикулярной оси Ох, получим в сечении некоторую плоскую фигуру с площадью

S=S(x).

Допустим, что функция S(x) непрерывна на  тогда объём V данного тела вычисляется по формуле:

                                                      (9)

где  – площадь поперечного сечения, соответствующего абсциссе х произвольной точки оси Ох, а  - абсциссы тех точек этой оси, через которые проходят плоскости, ограничивающие тело в направлении оси Ох.

Пример 9.

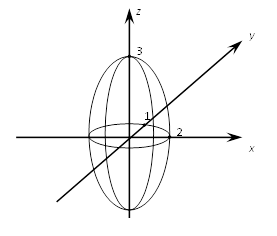Вычислить объём тела, заданного уравнением

Решение.

Данное тело является трёхосным эллипсоидом с полуосями

 оно заключено между секущими плоскостями, соответствующими значениям х=2 и х=2. Сечение эллипсоида плоскостью, перпендикулярной к оси Ох, представляет собой эллипс, уравнение которого имеет вид:

 или .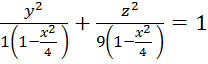

Полуоси этого эллипса будут

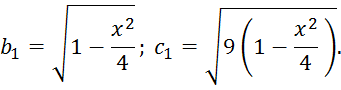
По известной формуле площади эллипса

находим площадь  поперечного сечения

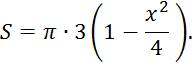
По формуле (9) искомый объём будет равен

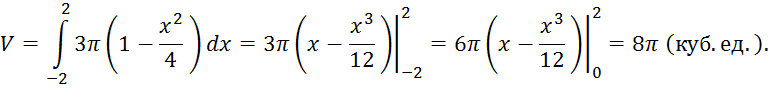
2. Объём тела вращения

а) Объем в прямоугольных координатах