I=![]()
Теорема существования определённого интеграла
Если функция f(x)
непрерывна на ![]() , то предел интегральной суммы
существует и не зависит от способа разбиения отрезка
, то предел интегральной суммы
существует и не зависит от способа разбиения отрезка ![]() на элементарные отрезки и от
выбора точек ξ.
на элементарные отрезки и от
выбора точек ξ.
 Числа
Числа ![]() соответственно называются нижним
и верхним пределами интегрирования.
соответственно называются нижним
и верхним пределами интегрирования.
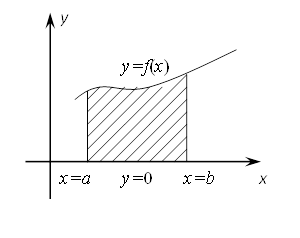
Если f(x)>0
на ![]() , то определённый интеграл
, то определённый интеграл ![]() геометрически представляют собой
площадь криволинейной трапеции – фигуры, ограниченной линиями y=f(x);
x=a;
x=b;
y=0;
геометрически представляют собой
площадь криволинейной трапеции – фигуры, ограниченной линиями y=f(x);
x=a;
x=b;
y=0;
Основные свойства определённого интеграла
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() (c-постоянная).
(c-постоянная).
6.
![]() :
:
если m ≤ f(x)
≤ M на ![]() , то m∙(b-a)
<
, то m∙(b-a)
<![]()
Правила вычисления определённых интегралов
1. Формула Ньютона – Лейбница:
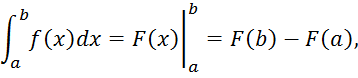
где
![]() - первообразная для
- первообразная для ![]() , т.е.
, т.е.
F′(x)=f(x).
2. Интегрирование по частям
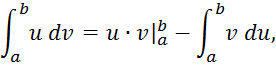
где
u=u(x),
v=v(x)
– непрерывно дифференцируемые функции на отрезке ![]() .
.
3. Замена переменной.
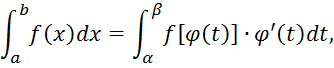
где ![]() функция, непрерывная вместе со
своей производной
функция, непрерывная вместе со
своей производной ![]() , на отрезке
, на отрезке ![]() ; a=
; a=![]() функция непрерывная на
функция непрерывная на ![]()
4.
Если
![]() - чётная функция, т.е.
- чётная функция, т.е. ![]() =
= ![]() , то
, то
![]() , если
, если ![]() - нечетная, т.е.
- нечетная, т.е. ![]() , то
, то ![]() .
.
Примеры:
1) Вычислить определённый интеграл до двух знаков после запятой
![]() dx
+ 3
dx
+ 3![]() dx
=
dx
=
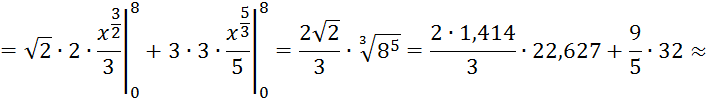
![]()
2) 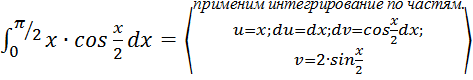 =
=
=x∙2∙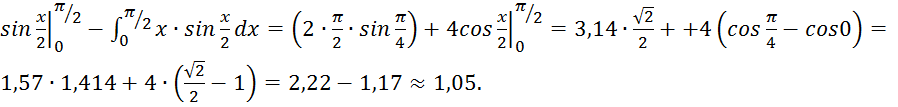
3)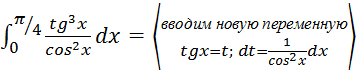 .
.
Тогда:
при х₁=0;
t₁=tg0=0, при х₂ =![]() , отсюда
, отсюда
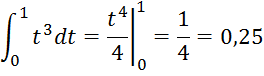
3) 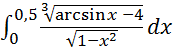 =
=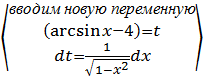 .
.
Тогда
при x₁=0; t=
arcsin 0 ![]() 4=
4=![]() 4
4
при x₂=0,5;
t= arcsin 0,5 ![]() 4 =
4 =![]()
получим
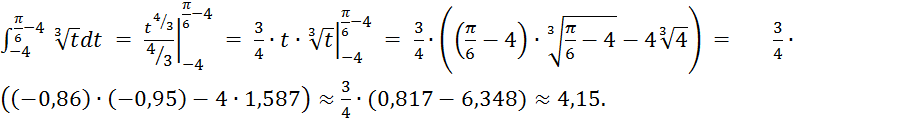
5)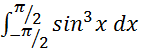 т.к. подынтегральная функция
нечётная
т.к. подынтегральная функция
нечётная
![]() , то согласно четвёртому правилу
, то согласно четвёртому правилу 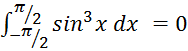 .
.
6) 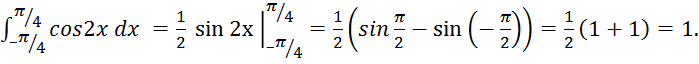
Т.к.
подынтегральная функция чётная, т.е. cos
2x=cos
(![]() 2x),
то можно также применить четвёртое правило вычисления, т.е.
2x),
то можно также применить четвёртое правило вычисления, т.е. 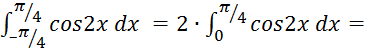
=![]() .
.
2.Приближённое интегрирование
Вычисление определённого интеграла по формуле Ньютона – Лейбница не всегда возможно, т.к. в ряде случаев не удаётся выразить первообразную для функции f(x) через элементарные функции в конечном виде. Вычисление же определённого интеграла, исходящее из определения его (т.е. как предела интегральных сумм) часто является невыполнимым из-за технических трудностей. В таких случаях прибегают к приближённому вычислению определённых интегралов, тем более что на практике часто и не требуется знать точное значение данного интеграла.
Рассмотрим некоторые способы приближённого вычисления определённых интегралов.
1.
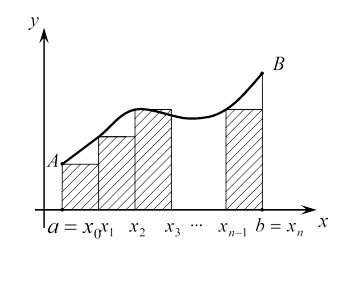 Способ прямоугольников.
Способ прямоугольников.
Пусть
функция y=f(x)
интегрируема на ![]() и требуется вычислить
и требуется вычислить
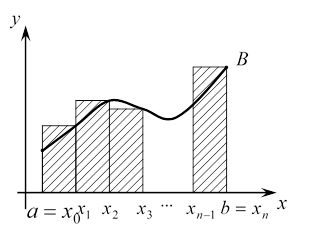 Разобьём сегмент
Разобьём сегмент ![]() на n
равных
частей точками x0=a,
x1,
x2,
…, xn-1,
xn=b.
Вычислим значения функции в каждой точке xi:
y0,
y1,
…, yn.
на n
равных
частей точками x0=a,
x1,
x2,
…, xn-1,
xn=b.
Вычислим значения функции в каждой точке xi:
y0,
y1,
…, yn.
Тогда
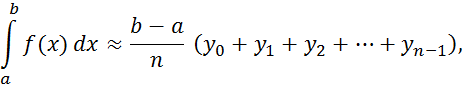
![]() (1)
(1)
Эти приближённые равенства называются формулами прямоугольников. Абсолютная величина погрешности Rn здесь
![]()
![]() , (2), где
М – такое число, что
, (2), где
М – такое число, что ![]()
Если погрешность ε задана, то число делений n выбирается так, чтобы выполнялось неравенство
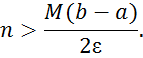
Пример 1. Вычислить по формулам прямоугольников интеграл
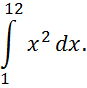
Решение.
Найдём сначала точное значение этого интеграла
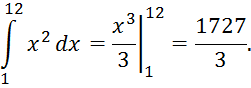
Разделим
сегмент ![]() на n=11
равных частей и вычислим значения xi
и yi
на n=11
равных частей и вычислим значения xi
и yi
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
yi |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
121 |
144 |
По формулам (1) получаем:
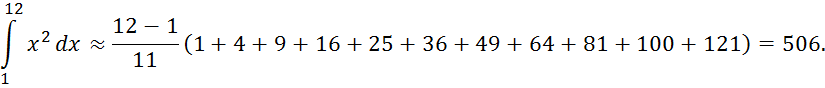
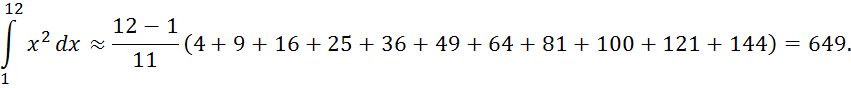
Абсолютные погрешности вычислений по этим формулам

Оценим погрешность вычисления по формуле (2).
Здесь
f′(x)=2x.
Поэтому на сегменте ![]() , следовательно
, следовательно
![]() .
.
Итак, способ прямоугольников самый простой и вместе с тем наиболее грубый способ приближённого интегрирования.
2.
 Способ трапеций.
Способ трапеций.
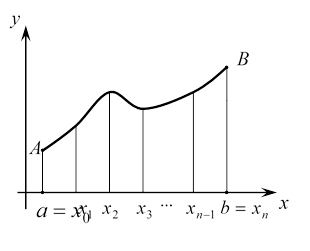
Пусть снова требуется вычислить
Разобьём
![]() на n
равных
частей и сохраним введённые выше обозначения.
на n
равных
частей и сохраним введённые выше обозначения.
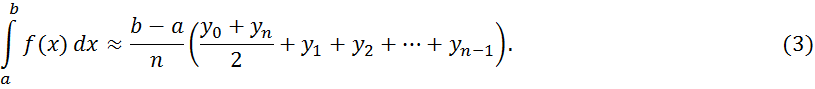
Равенство
(3) называется формулой трапеций. Для нее абсолютная погрешность ![]() определяется
определяется
![]() (4)
(4)
где
М – наибольшее значение f![]() (x)
на
(x)
на ![]() .
.
Если требуется точность ε, то число n выбирается
n<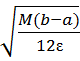 .
.
Пример 2.
Вычислим
по формуле трапеций интеграл ![]() который мы уже вычислим по
формулам прямоугольников.
который мы уже вычислим по
формулам прямоугольников.
Решение.
Возьмём, как и прежде, n=11, тогда по формуле (3) получаем:
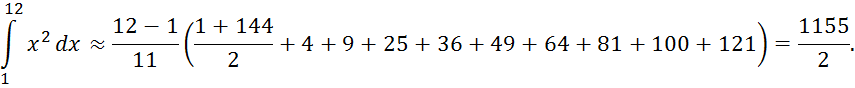
Абсолютная
погрешность результата равна ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.