Таким образом, формула трапеций даёт результат значительно точнее, чем формулы прямоугольников.
3. Способ парабол (Симпсона).
Пусть
требуется вычислить ![]()
Разбив
![]() на 2n
равных частей и сохранив введённые выше обозначения, имеем
на 2n
равных частей и сохранив введённые выше обозначения, имеем
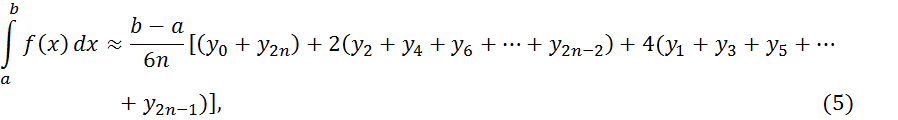
Это так называемая формула парабол (формула Симпсона).
Абсолютная погрешность R2n:

где
М – наибольшее значение ![]()
Пример 3.
Вычислить приближённо
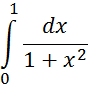
Решение.
Найдём сначала точное значение этого интеграла по формуле Ньютона – Лейбница
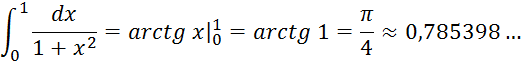
Вычислим теперь приближённое значение его по формулам (1) и (3). Пусть n=10.
|
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
|
1,00000 |
0,99010 |
0,96154 |
0,91743 |
0,86207 |
0,80000 |
0,73529 |
0,67114 |
0,60976 |
0,55249 |
0,50000 |
По второй формуле прямоугольников получим ![]() Верен только один десятичный знак.
Верен только один десятичный знак.
По формуле трапеций (3) получим ![]() верны уже два десятичных знака.
верны уже два десятичных знака.
Теперь вычислим этот интеграл по формуле Симпсона,
для чего разделим сегмент ![]() всего на 4 части, тогда
всего на 4 части, тогда
|
|
0 |
|
|
|
|
|
|
1,0 |
0,94118 |
0,8 |
0,64 |
0,5 |
Согласно формуле (5) получаем:
![]() где все пять десятичных знаков
верны.
где все пять десятичных знаков
верны.
Задание 2.
Вычислить точное значение определённого интеграла I по формуле Ньютона – Лейбница. Вычислить этот же интеграл приближёнными способами: в способах прямоугольников и трапеций задать n=10, в способе парабол n=4. Найти относительные погрешности приближённых вычислений δ1, δ2 и δ3.
Примечание.
δ=![]() где
где ![]() - абсолютная погрешность,
- абсолютная погрешность,
x - точное значение.
3. Приложение определённого интеграла к задачам геометрии
3.1 Вычисление площадей плоских фигур
1. Площадь в прямоугольных координатах
При постановке задачи определённого интегрирования
было показано, что определённый интеграл в случае, когда ![]() , с геометрической точки зрения
определяет площадь криволинейной трапеции
, с геометрической точки зрения
определяет площадь криволинейной трапеции ![]() , т.е. фигуры , ограниченной
, т.е. фигуры , ограниченной 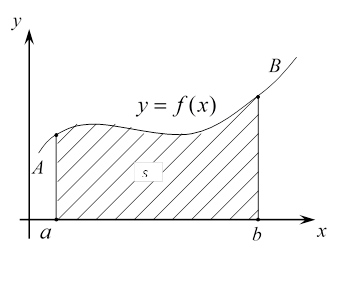 прямыми
прямыми
![]() и кривой
и кривой ![]() , где
, где ![]() - неотрицательная, непрерывная на
- неотрицательная, непрерывная на ![]() функция.
функция.
![]() (1)
(1)
Площадь всякой плоской фигуры можно рассматривать как сумму или разность площадей некоторых криволинейных трапеций. Это означает, что с помощью определённых интегралов можно вычислить площади любых плоских фигур.
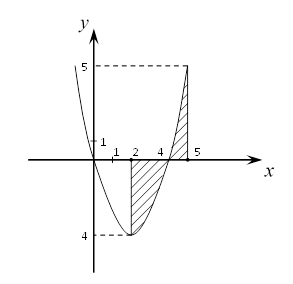
Пример 1.
Вычислить
площадь фигуры, ограниченной линиями ![]()
Решение.
Вначале построим фигуру, ограниченную данными линиями, предварительно приведя уравнение параболы к каноническому виду.
![]()
![]()
Это парабола с вершиной в точке О′(2;-4), ветви
направлены вверх, параметр ![]() .
.
Искомая площадь ![]() поэтому
поэтому 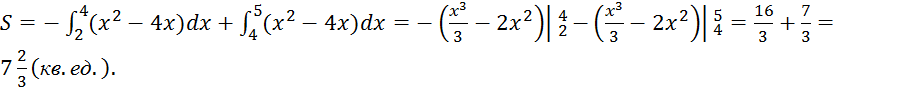
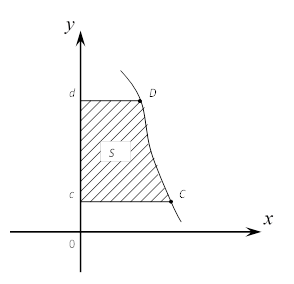 Фигуру, ограниченную прямыми
Фигуру, ограниченную прямыми ![]() и кривой
и кривой ![]() , где
, где ![]() также называют криволинейной
трапецией
также называют криволинейной
трапецией ![]() . Площадь её вычисляется по
формуле
. Площадь её вычисляется по
формуле
![]() (2)
(2)
Пример 2.
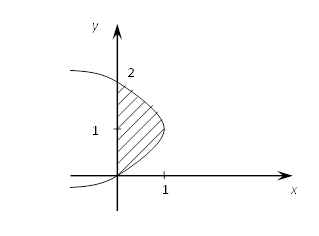 Вычислить
площадь фигуры, ограниченной осью Оу и параболой
Вычислить
площадь фигуры, ограниченной осью Оу и параболой ![]()
Решение.
Найдём сначала ординаты точек пересечения параболы с осью Оу:
![]()
Находим площадь по формуле (2)
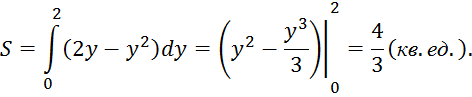
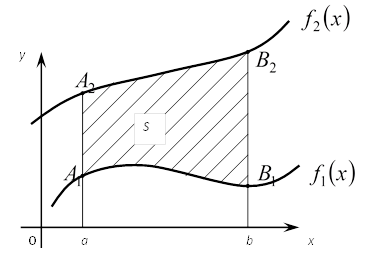 Площадь фигуры, ограниченной двумя кривыми
Площадь фигуры, ограниченной двумя кривыми ![]() и
и ![]() и двумя вертикальными прямыми
и двумя вертикальными прямыми ![]() причём
причём ![]() при
при ![]() очевидно, легко вычислить как
разность площадей криволинейных трапеций
очевидно, легко вычислить как
разность площадей криволинейных трапеций ![]() и
и ![]() т.е.
т.е.
![]() (3)
(3)
Пример 3.
Вычислить
площадь фигуры, ограниченной линиями ![]()
Решение.
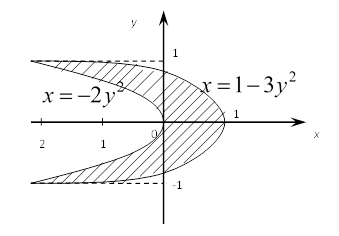 Приведём
уравнения парабол к каноническому виду:
Приведём
уравнения парабол к каноническому виду:
![]() – парабола, вершина в т. О (0;0),
ветви направлены влево, параметр
– парабола, вершина в т. О (0;0),
ветви направлены влево, параметр ![]()
![]() – парабола, вершина в т. О′ (1;0),
ветви направлены влево, параметр
– парабола, вершина в т. О′ (1;0),
ветви направлены влево, параметр ![]()
Найдём точки пересечения, приравняв уравнения парабол:
![]()
![]()
Из рисунка видно, что для вычисления площади данной фигуры удобнее интегрировать по оси Оу:
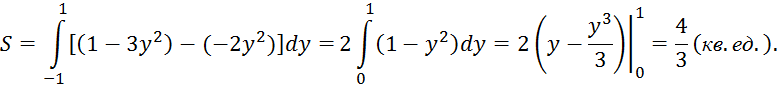
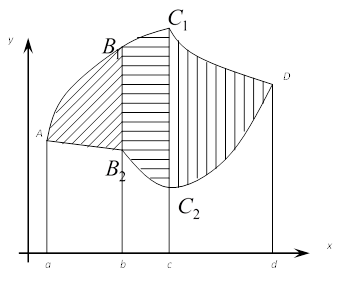 Когда плоская фигура ограничена дугами нескольких
кривых, её разбивают на части прямыми, параллельными оси Ох ( или оси Оу) так,
чтобы к вычислению площади каждой полученной части можно было применить
используемые ранее формулы. Площадь всей фигуры вычисляется как алгебраическая
сумма площадей частей, на которые оказалась разбитой данная фигура.
Когда плоская фигура ограничена дугами нескольких
кривых, её разбивают на части прямыми, параллельными оси Ох ( или оси Оу) так,
чтобы к вычислению площади каждой полученной части можно было применить
используемые ранее формулы. Площадь всей фигуры вычисляется как алгебраическая
сумма площадей частей, на которые оказалась разбитой данная фигура.
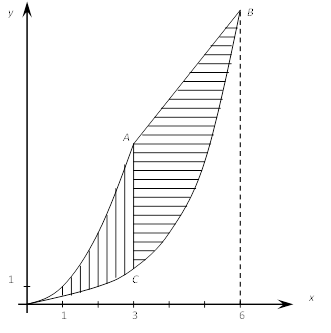 Пример
4.
Пример
4.
Вычислить
площадь фигуры, ограниченной линиями ![]() ,
, ![]()
Решение.
Решая системы:
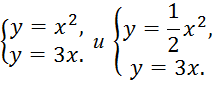
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.