Определенный интеграл и его приложения, страница 5

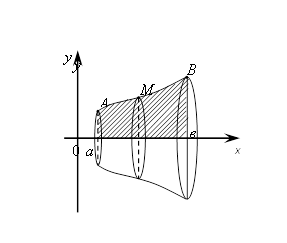
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная осью Ох, прямыми х = а и х =b  и дугой АВ кривой y=f(x); где f(x) – непрерывная, неотрицательная на  функция. Тогда эта трапеция опишет тело, являющееся телом вращения.

Так как каждая точка М дуги АВ описывает окружность, то сечение тела вращения плоскостью, перпендикулярной к оси Ох, представляет собой круг радиуса y=f(x), и значит его площадь

.

Таким образом, используя формулу (9) получаем объем тела вращения:

.                                    (10)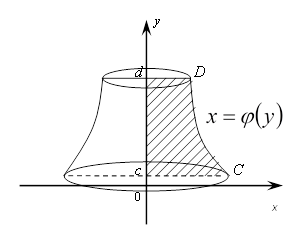

Если тело образуется вращением криволинейной трапеции с CDd  вокруг оси Оу, то объём такого тела, очевидно, будет вычисляться по формуле

.(10′)

Пример 10.

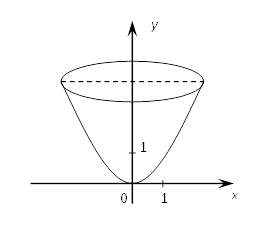Вычислить объём тела, образованного вращением вокруг оси Оу криволинейной трапеции, ограниченной осью Оу, кривой  и прямой y=3.

Решение.

Т.к. тело образовано вращением вокруг оси Оу, воспользуемся формулой (10′). Поскольку , то  

.

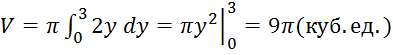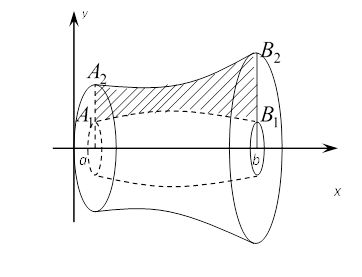Если вокруг оси Ох вращается фигура А₁А₂В₂В₁, ограниченная двумя кривыми:  и () и двумя прямыми x=aи x=b, то объём V полученного кольцеобразного тела вращения, определяется как разность двух объёмов:

               (11).

Аналогично, если тело образовано вращением вокруг оси Оу фигуры, ограниченной кривыми  и   () и прямыми y=c и y=d, то для вычисления объёма такого тела пользуются формулой

                                (11′).

Пример 11.

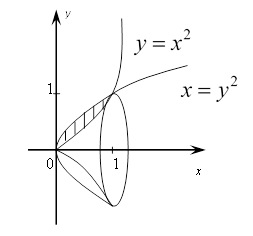Вычислить объём тела, полученного вращением вокруг оси Ох фигуры, лежащей в плоскости ХОУ и ограниченной линиями.

Решение.

Находим точки пересечения кривых  это точки

По формуле (11) находим объём тела вращения, учитывая, что в данном случае

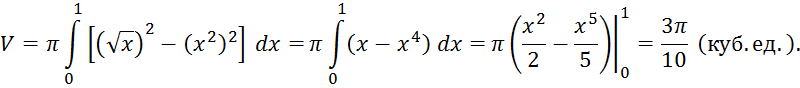
б) Объём тела вращения в случае параметрического задания кривых.

Пусть кривая, дугой АВ которой ограничена вращающаяся вокруг оси Ох криволинейная трапеция, задана параметрически:

Тогда объём тела вращения вычисляется по формуле

                                    (12)

где Т - значения параметра t, соответствующего точкам А и В.

Пример 12.

Вычислить объём веретенообразного тела, производимого вращением вокруг оси Ох фигуры, ограниченной астроидой:

Решение.

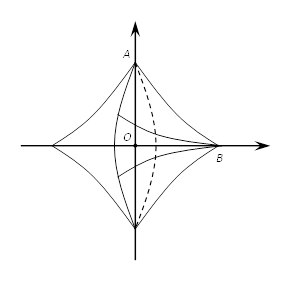Из соображений симметрии будем вычислять половину искомого объёма, например объём V₁ тела, образованного вращением фигуры ОАВ вокруг оси Ох. Т.к. абсциссы точек А и В соответственно равны 0 и 1, то пределы интегрирования  Т находим из уравнений:

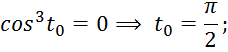
Находим далее .

По формуле (12) получаем

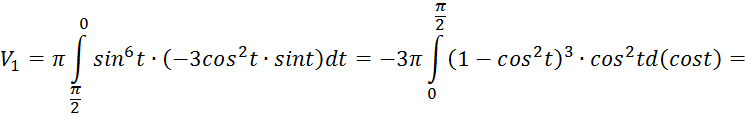
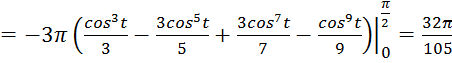  (куб. ед.).

3.4. Вычисление площади поверхности вращения

а) Площадь поверхности вращения в декартовых координатах

Пусть дуга АВ кривой  где  - непрерывно дифференцируемая функция, вращается вокруг оси ОХ. Тогда площадь Р полученной поверхности вращения вычисляется по формуле :

                                (13).

Здесь a и b – абсциссы концов кривой АВ, точек А и В соответственно.

Аналогично, если кривая задана уравнением  (c и d соответственно, ординаты точек С и D концов дуги CD), то площадь поверхности вращения вычисляется:

                                (13′).

Пример 13.

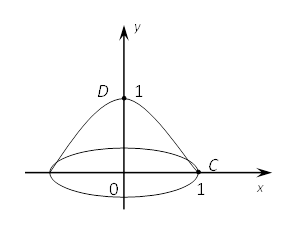Вычислить площадь поверхности, образованной вращением вокруг оси ОУ дуги кривой  расположенной над осью абсцисс.

Решение.

Дуга CD содержится между точкой с ординатой  и  это и есть пределы интегрирования. Здесь . По формуле (13′) имеем:

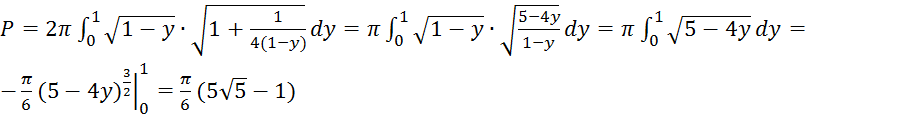(кв.ед.).

б) Площадь поверхности вращения в случае, когда кривая задана параметрически

Если кривая, дуга АВ которой вращается вокруг оси ОХ, задана параметрическими уравнениями  причём  и  и   непрерывны на  и   то площадь поверхности вращения вычисляется по формуле:

                      (14).

Пример 14.

Вычислить площадь поверхности, образованной вращением вокруг оси ОХ одной арки циклоиды

Решение.

Находим  по формуле (14) получаем

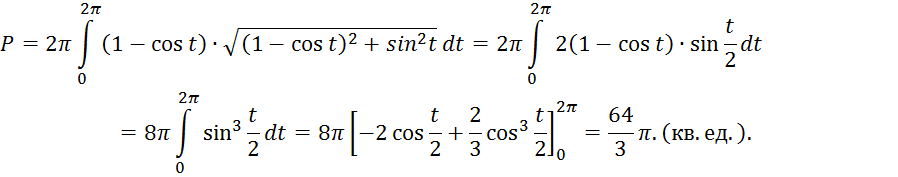
в) Площадь поверхности вращения в случае полярных координат

Если кривая задана в полярных координатах уравнением ,  непрерывна на  и то площадь поверхности вращения вычисляется по формуле

                                 (15)

Пример 15.

Определить площадь поверхности, образованной вращение кардиоиды  вокруг полярной оси.

Решение.

Т.к. кардиоида симметрична относительно полярной оси, то искомую поверхность может быть получена и вращением дуги, описывающей верхнюю половину кардиоиды, около той же оси. Тогда пределы интегрирования по  будут равны 0 и π. По формуле (15) получаем: