Билет 17
![]() 1. Интеграл
по фигуре и его свойства.
1. Интеграл
по фигуре и его свойства.
2.![]()
 C
C
B
![]()
![]()

A
П=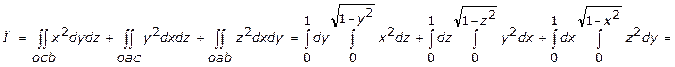
![]()
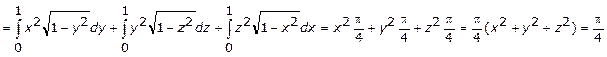
3.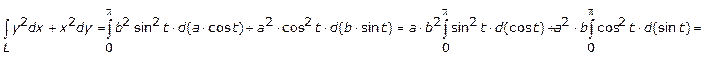
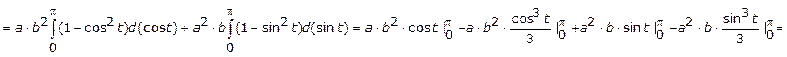
![]()
4. Характеристический многочлен. Решение линейных ДУ с постоянными коэффициентами в случае различных действительных и комплексных корней.
![]()
![]()
![]() Многочлен det(λΕ−Α)
n-й степени относительно λ называется характеристическим многочленом матрицы
A, A=
Многочлен det(λΕ−Α)
n-й степени относительно λ называется характеристическим многочленом матрицы
A, A=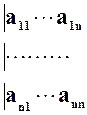 . Уравнение
. Уравнение ![]() наз.
характеристическим уравнением ЛОДУ. Для построения системы решения ЛОДУ надо
найти его корни, при этом возможны 4 случая: 1)
наз.
характеристическим уравнением ЛОДУ. Для построения системы решения ЛОДУ надо
найти его корни, при этом возможны 4 случая: 1)![]() –
действительный простой корень, то решение
–
действительный простой корень, то решение ![]() ; 2)
; 2) ![]() – действительный корень кратный m, m>1, то решение
– действительный корень кратный m, m>1, то решение ![]() 3)
3)![]() –пара
комплексно
–пара
комплексно
сопряженных
корней им соответствует решение ![]()
4) ![]() комплексно сопряженные корни кратности m>1, то решение будут
комплексно сопряженные корни кратности m>1, то решение будут 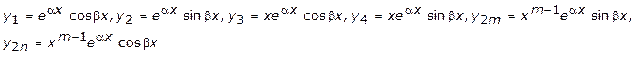
5. Понятие
устойчивости решения системы линейных ДУ с постоянными коэффициентами. ![]() (1) –рассмотрим
систему ДУ
(1) –рассмотрим
систему ДУ 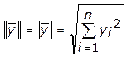
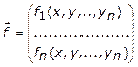 .
.
Определение: Решение ![]() системы (1)наз. устойчивым полем Ляпунова
при
системы (1)наз. устойчивым полем Ляпунова
при ![]() , если для любого
, если для любого ![]() >0
можно указать положительные
>0
можно указать положительные ![]() >0, что при x>x0
для любого решения
>0, что при x>x0
для любого решения ![]() системы (1) будет иметь место
неравенство
системы (1) будет иметь место
неравенство ![]() <
<![]() , если
имеет место неравенство
, если
имеет место неравенство ![]() <
<![]() . Если кроме того справедливо
. Если кроме того справедливо ![]() =0, при достаточно малых значениях
=0, при достаточно малых значениях ![]() , то решение
, то решение![]() системы
(1)наз. асимптотически устойчивым при
системы
(1)наз. асимптотически устойчивым при ![]() . Лемма:
Пусть для некоторого
. Лемма:
Пусть для некоторого ![]() >0 функции
>0 функции ![]() определены и непрерывны при x>x0>+
определены и непрерывны при x>x0>+![]()
![]() и
и 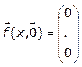 . Пусть
при тех же
. Пусть
при тех же ![]() существует непрерывно диффириенцируемая функция
Ляпунава
существует непрерывно диффириенцируемая функция
Ляпунава ![]() , которая не отрицательна и равна нулю лишь
в начале координат, причем данная функция должна удовлетворять условию, тогда
, которая не отрицательна и равна нулю лишь
в начале координат, причем данная функция должна удовлетворять условию, тогда![]() системы (1) тождественно является
устойчивым. Если кроме того, при тех же y1, y2,…yn имеет
место неравенство
системы (1) тождественно является
устойчивым. Если кроме того, при тех же y1, y2,…yn имеет
место неравенство![]() , где функция
, где функция ![]() некоторая непрерывная функция равная нулю
лишь в начале координат, то нулевое решение будет асимптотически устойчивым.
некоторая непрерывная функция равная нулю
лишь в начале координат, то нулевое решение будет асимптотически устойчивым.
6.
![]()
x2+2x+1= 0
![]()
![]()
![]()
![]()
2
![]()
1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
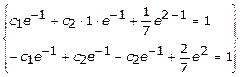
![]() ;
; ![]()
Ответ:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.