Билет 1
1. Интеграл по фигуре и его свойства.
2. Линейная независимость функций. Определитель Вронского.
Опр:
Функции ![]() наз. линейно-независимыми на
наз. линейно-независимыми на ![]() , если только при
, если только при ![]() выполняется
равенство:
выполняется
равенство: ![]() . В противном случае функции явл.
линейно-зависимыми.
. В противном случае функции явл.
линейно-зависимыми.
Теорема:
Если функции ![]() линейно-зависимы на
линейно-зависимы на ![]() , то определитель Вронского тождественно
равен нулю на этом отрезке :
, то определитель Вронского тождественно
равен нулю на этом отрезке :
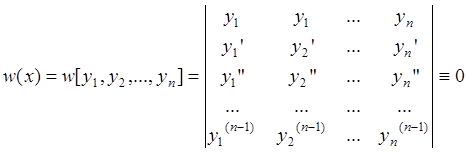 .
.
Док-во:
так как функции ![]() линейно-зависимы на
линейно-зависимы на ![]() , то по определению на этом отрезке
справедливо тождество
, то по определению на этом отрезке
справедливо тождество ![]()
![]() ,
причем не все
,
причем не все ![]() равны нулю.
равны нулю.
Продифференцируем
это тождество ![]() раз:
раз:
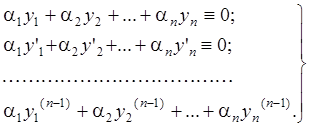
при
любом ![]() получаем линейную однородную систему
алгебраических уравнений относительно
получаем линейную однородную систему
алгебраических уравнений относительно ![]() неизвестных
неизвестных
![]() . Поскольку эта система имеет ненулевое
решение (не все
. Поскольку эта система имеет ненулевое
решение (не все ![]() равны нулю), то как известно,
определитель ее равен нулю (из теоремы Крамера). Следовательно, определитель
системы (опр. Вронского) равен нулю в каждой точке
равны нулю), то как известно,
определитель ее равен нулю (из теоремы Крамера). Следовательно, определитель
системы (опр. Вронского) равен нулю в каждой точке ![]() .
.
3. 
4. Решение нормальной системы n-ДУ I-го порядка методом Эйлера.
Опр:
систему ДУ 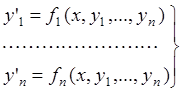 наз. нормальной сист. ДУ.
наз. нормальной сист. ДУ.
5.
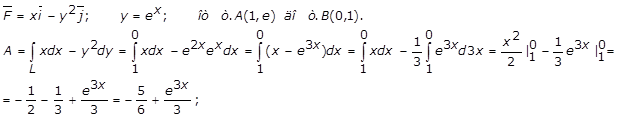
Билет 2
1. Вычисление криволинейного интеграла I-го рода.
КРИ-1 равен 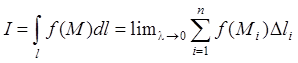 . Если кривая
. Если кривая ![]() кусочно-гладкая,
а функция
кусочно-гладкая,
а функция ![]() на ней непрерывна, то данный интеграл
существует.
на ней непрерывна, то данный интеграл
существует.
1) Пусть
кривая ![]() плоская и задана уравнением
плоская и задана уравнением ![]() ,
, ![]() , где
, где ![]() – диф. функция, тогда:
– диф. функция, тогда: ![]() , в итоге получим :
, в итоге получим : 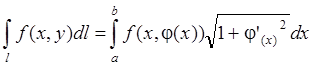 .
.
2) ![]() – плоская кривая, заданная уравнением:
– плоская кривая, заданная уравнением: ![]() ,
, ![]() , тогда:
, тогда:
![]()
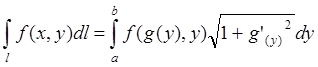
3) ![]() – плоская кривая, заданная параметр.
ур-ями:
– плоская кривая, заданная параметр.
ур-ями: 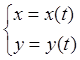 ,
, ![]() :
: ![]() ;
; 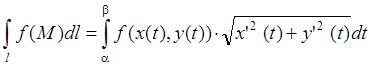 .
.
4) ![]() – плоская кривая, заданная в полярных
координатах
– плоская кривая, заданная в полярных
координатах
![]() ,
, ![]() :
: ![]()
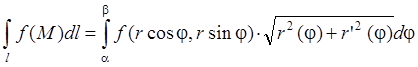 .
.
5) ![]() – пространственная кривая , заданная
параметрическими уравнениями
– пространственная кривая , заданная
параметрическими уравнениями 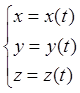 ,
,![]() :
:
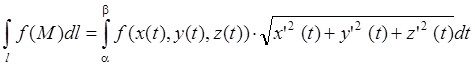 .
.
2. Поток векторного поля.
Поток
– количество жидкости (газа) протекающее через ориентированную поверхность ![]() в единицу времени.
в единицу времени.
Пусть
в каждой точке поверхности ![]() задана векторная
функция:
задана векторная
функция: ![]() ,
, ![]()
![]() – поток через
– поток через ![]() , с
точностью до бесконечно малых элементарный поток будет равен
, с
точностью до бесконечно малых элементарный поток будет равен ![]() – произведение проекции на нормаль вектора
скорости на площадь поверхности.
– произведение проекции на нормаль вектора
скорости на площадь поверхности.
 , Пусть
, Пусть ![]() , тогда
в пределе получаем:
, тогда
в пределе получаем: 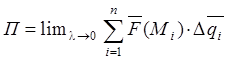
ОПР:
Предел , не зависящий от способа построения суммы наз. поверхностным интегралом
второго рода от векторной функции ![]() по ориентированной
поверхности
по ориентированной
поверхности ![]() и обозначают:
и обозначают: 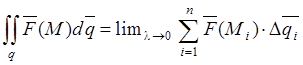 ,
механический смысл которого – поток.
,
механический смысл которого – поток.
В
координатной форме : 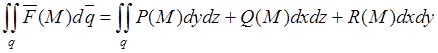 .
.
Билет 3
1. Вычисление
тройного интеграла в декартовых координатах. Пусть ![]() является
цилиндрическим телом, проекция которого на плоскость
является
цилиндрическим телом, проекция которого на плоскость ![]() есть
область
есть
область ![]() и которое ограничено снизу поверхностью
и которое ограничено снизу поверхностью ![]() , а сверху v поверхностью
, а сверху v поверхностью ![]() , где
, где
![]() - непрерывные функции в . Тогда
- непрерывные функции в . Тогда  , то
есть интегрированием по z тройной интеграл сводится к двойному интегралу по
области
, то
есть интегрированием по z тройной интеграл сводится к двойному интегралу по
области ![]() . Для областей более сложной формы вычисление
двойных и тройных интегралов производится разбиением областей на конечное число
простых областей с уже рассмотренными свойствами.
. Для областей более сложной формы вычисление
двойных и тройных интегралов производится разбиением областей на конечное число
простых областей с уже рассмотренными свойствами.
2.
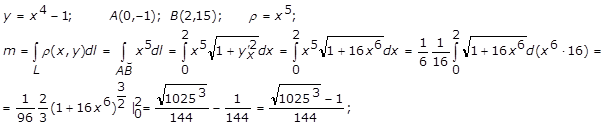
3.
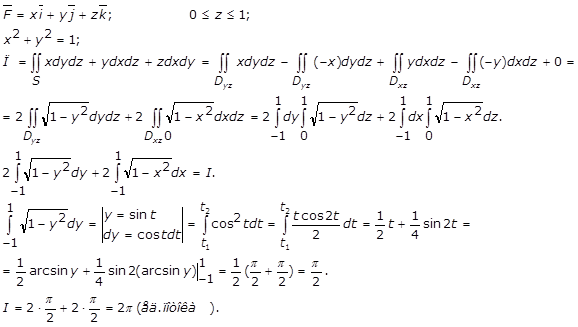
4. Уравнения, разрешенные относительно производной порядка n : ![]() .
.
5.
Теорема о структуре общего решения неоднородного линейного ДУ. Пусть![]() =l1y1+…+lnyn (li–произвольные
постоянные), общее решение однородного уравнения L(y)=0(2) y*–частное решение
неоднородного уравнения yn+a1(x)y(n-1)+..+an-1(x)
=l1y1+…+lnyn (li–произвольные
постоянные), общее решение однородного уравнения L(y)=0(2) y*–частное решение
неоднородного уравнения yn+a1(x)y(n-1)+..+an-1(x)![]() +an(x)y=f(x)(1), тогда общее
решение уравнения (1) имеет вид
+an(x)y=f(x)(1), тогда общее
решение уравнения (1) имеет вид ![]() (3).
(3).
Доказательство:
1) L(![]() )=L(
)=L(![]() )+L(
)+L(![]() )=f(x)
)=f(x) ![]() ci
ci
2) Рассмотрим начальное условие ![]() (4)
(4)
Покажем,
что любое решение задачи Коши (1),(4) может быть получено из формулы (3) при
подходящих значениях ci=ci0, i=![]() . Решение задачи Коши (1), (4) обозначим y0(x), покажем что его
можно получить из формулы (3).
. Решение задачи Коши (1), (4) обозначим y0(x), покажем что его
можно получить из формулы (3).
![]() =
=![]() ,
, ![]() по свойству L(
по свойству L(![]() )=L(
)=L(![]() )-L(
)-L(![]() )=0 решение однородного уравнения (2).
Поскольку
)=0 решение однородного уравнения (2).
Поскольку ![]() –общее решение уравнения (2), то при
подходящих значениях li0 будем
иметь
–общее решение уравнения (2), то при
подходящих значениях li0 будем
иметь ![]()
![]()
Билет 4
1. Поверхностный интеграл ΙΙ-го рода и его
свойства. Если поверхность задана уравнением ![]() и
однозначно проектируется на плоскость
и
однозначно проектируется на плоскость ![]() , то
поверхностный интеграл 1-го рода вычисляется по формуле
, то
поверхностный интеграл 1-го рода вычисляется по формуле  .
Нетрудно получить аналогичные формулы, если поверхность однозначно
проектируется на другие координатные плоскости. Поскольку вычисление
поверхностного интеграла сводится к двойному интегралу, то, естественно, все
свойства поверхностного интеграла 1-го рода такие же, как и у двойного.
.
Нетрудно получить аналогичные формулы, если поверхность однозначно
проектируется на другие координатные плоскости. Поскольку вычисление
поверхностного интеграла сводится к двойному интегралу, то, естественно, все
свойства поверхностного интеграла 1-го рода такие же, как и у двойного.
2. Формула Стокса. Рассмотрим кусочно-гладкую поверхность S ограниченную замкнутым контуром L. Выберем нормаль n и направление обхода контура l так, чтобы со стороны нормали обход выполнялся против часовой стрелки. Пусть в точках поверхности S, включая границу l, определена непрерывная векторная
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.