Математика \ Высшая математика

Теория множеств. Отображения. Мощности множеств и комбинаторика

Страницы работы

8 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

I. ТЕОРИЯ МНОЖЕСТВ

§ 1. Множества

1.1. Верно ли равенство множеств , если

а) , ;

б) , ;

в) , ;

г) , ;

д) , ;

е) , .

1.2. Найдите множества , , \, \ и дайте (в случае бесконечных множеств) их геометрическую интерпретацию, если

а) , ;

б) , ;

в) , ;

г) , ;

д) , .

1.3. Пусть F – множество решений уравнения , а G – множество решений уравнения . С помощью операций над множествами представьте множество решений уравнения:

а) ;

б) ;

в) ;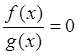

1.4. Найдите множества , , , , и дайте (в случае бесконечных множеств) их геометрическую интерпретацию, если

а) , ;

б) , ;

в) , .

1.5. Каким условиям должны удовлетворять множества и , чтобы

а) ;

б) ;

в) .

1.6. Пусть -- универсальное множество; и -- его подмножества. Докажите, что следующие утверждения:

а) ;

б) ;

в) .

1.7. Пусть , и С -- произвольные множества. Какие из следующих равенств являются верными:

а) ;

б) ;

в) ?

1.7. Докажите тождества:

а) ;

б) ;

в) .

1.8. Докажите, что для любых множеств A, B и C

а) если , то ;

б) если , то ;

в) ;

г) ;

д) .

1.9. Разностная сумма множеств (или сумма по модулю 2) определяется следующим равенством: . Найдите формулы, которые могут служить другими эквивалентными определениями этой операции. Докажите следующие свойства:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

1.10. В потоке учится 100 студентов. 28 из них изучают английский язык, 30 – немецкий, 42 – французский. При этом известно также, что 8 студентов изучают параллельно английский и немецкий языки, 10 – английский и французский, 5 – немецкий и французский, а 3 студента изучают все три названных языка. Определите, сколько студентов

а) изучают только английский язык;

б) изучают только немецкий язык;

в) изучают только французский язык;

г) не изучают ни одного из названных языков.

1.11. В потоке учится 100 студентов. 26 из них изучают немецкий язык, 48 – французский. При этом известно также, что 8 студентов изучают параллельно и немецкий, и французский языки, 18 – только немецкий, а 24 студента не изучают ни одного из названных языков. Сколько студентов изучают только английский язык?

§ 2. Отображения

2.1. Пусть R– множество действительных чисел и заданы следующие отображения:

, ; , ;

, ; , .

Найдите , , , , , , , ,, , , ,, . Существуют ли среди заданных и найденных отображений равные?

2.2. Пусть , . Найдите число всех отображений . При каких n и m существует

а) инъективное отображение ;

б) сюръективное отображение ;

в) биективное отображение ?

2.3. Пусть X – конечное множество. Докажите, что отображение сюръективно тогда и только тогда, когда оно инъективно.

2.4. Какие из следующих отображений являются инъективными, сюръективными, биективными:

а) , ;

б) , (здесь N– множество натуральных чисел);

в) , ;

г) , ;

д) , ;

е) , (здесь -- множество положительных действительных чисел);

ж) , ;

з) , ;

и) , ;

к) , ;

л) , ;

м) , .

Какие из перечисленных отображений обратимы? Для них найдите обратные отображения.

2.5. Пусть -- произвольное отображение. Докажите, что для любых и :

а) если , то;

б) ;

в) (приведите пример, когда не верно обратное включение);

г) тогда и только тогда, когда отображение -- инъективно.

2.6. Пусть -- такое отображение, что для некоторого натурального n. Докажите, что f – биекция.

§ 3. Мощности множеств и комбинаторика

3.1. Для мощности объединения двух конечных множеств справедлива формула . Найдите аналогичную формулу для мощности объединения трех конечных множеств.

3.2. а) Пусть и . Найдите число биективных отображений (см. задачу 2.2 в))

б) Пусть , а , (см. 2.2 а)). Найдите число инъективных отображений .

3.3. Сколько существует способов расположить n предметов по кругу?

3.4. Сколько различных слов можно получить путем перестановки букв в слове МАТЕМАТИКА?

3.5. Сколько существует способов рассадить за круглым столом n мужчин и n женщин, чтобы мужчины и женщины чередовались?

3.6. Сколько существует способов выбрать из n депутатов комиссию, состоящую из m человек, и ее председателя?

3.7. В студенческой группе 30 человек. Сколько существует способов разбить ее на две а) равные по численности, б) произвольные подгруппы и в каждой подгруппе выбрать старосту?

3.8. Пусть -- число сочетаний из n элементов по m. Докажите, справедливость следующих формул:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .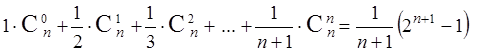

3.9. Множество X состоит из 5 элементов. Найдите число разбиений этого множества на непустые подмножества.

3.10. Прямая разбита на отрезки. Какую мощность может иметь полученное множество отрезков?

3.11. Определите мощность множества алгебраических чисел. (Число называется алгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами.)

4. Отношения

4.1. На множестве задано бинарное отношение . Найдите область определения и множество значений этого отношения. Является ли оно функциональным, рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, связным, если для любых по определению означает:

а) ;

б) ;

в) ;

г) ;

д) ;

е) (a делится на b);

4.2. На множестве натуральных чисел Nзадано бинарное отношение . Найдите область определения и множество значений этого отношения. Является ли оно функциональным, рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, связным, если для любых по определению означает: