Теория множеств. Отображения. Мощности множеств и комбинаторика, страница 2

4.4.  Какие из следующих отношений являются функциональными:

а)   ;

б)   ;

в)   ;

г)   ;

д)   ;

е)   ;

ж)   .

4.5. Что можно сказать об отношениях  и , если отношение

а)  рефлексивно;     б) симметрично;    в)  антисимметрично;      г)  транзитивно.

4.6.  Пусть  и  -- бинарные отношения на множестве натуральных чисел. Найдите , , , , , , если

а)  ,  ;

б) ,  ;

в)  ,      .

4.7.  Пусть  и  -- отношения на множествах  X  иY.  Докажите, что

а)  ;

б)  ;

в)  ;

г)  ;

д)  .

4.8.  Пусть  -- бинарное отношение на множестве  X.  Докажите, что  свойства рефлексивности, симметричности и транзитивности равносильны соответственно:

а)  ;             б)  ;          в)  .

4.9.  Докажите, что для любого бинарного отношения  на множестве  X  отношения  и  являются симметричными. 

4.10. Докажите, что  бинарное отношение  тогда и только тогда является отношением эквивалентности, когда   а) ,    б)   и   в) .

4.11.  Пусть  и  -- отношения частичного порядка на множестве  X.  Докажите или опровергните, что   и  также являются отношениями  а) эквивалентности, б) частичного порядка.

4.12.  Докажите, что если  -- рефлексивное и транзитивное отношение на множестве  X,  то    являются отношением эквивалентности. 

4.13. Докажите, что  бинарное отношение  тогда и только тогда является отношением частичного порядка, когда   а) ;   б)    и   в) .

5.  Алгебраические структуры

5.1.  Исследуйте свойства операции  на  множестве M. Какую алгебраическую структуру образует это множество относительно данной операции?

а)   M = R,;

б)   M = N,;

в)  M = N,;

г)   M = N, ;

д)   M = Q \ {0},;

е)   M = 3Z = { 3a | aÎZ } , ;

ж)  ,;

 з)  ,  .

5.2.    Определите, какую структуру образует следующее множество относительно указанной операции:

а) множество векторов в трехмерном пространстве с операцией векторное произведение;

б) множество векторов в трехмерном пространстве с операцией сумма векторов;

в) множество векторов в трехмерном пространстве с операцией скалярное произведение;

г)  множество всех отображений  с операцией произведение (композиция) отображений;

д)  множество биективных отображений  с операцией произведение (композиция) отображений;

е)  множество  четных подстановок из n  элементов относительно операции произведение подстановок;

ж) множество всех отношений на множестве  с операцией произведение отношений;

з) множество верхних треугольных матриц порядка n c действительными элементами относительно операции сложение (умножения) матриц;

и) множество диагональных матриц порядка n c действительными элементами относительно операции сложение (умножения) матриц;

к) множество невырожденных квадратных  матриц порядка n c действительными элементами относительно операции произведение матриц;

л) множество квадратных матриц порядка n c целыми элементами и определителем относительно операции произведение матриц;

м) множество квадратных матриц порядка n, у которых в каждойстрочке и каждом столбце ровно один ненулевой элемент, равный 1, относительно операции произведение матриц;

н) множество всех подмножеств универсального множества U  c операцией пересечение (объединение, разностная сумма) множеств;

5.3.  Пусть  -- n-ая декартова степень множества  . Задайте на  бинарную операцию так, чтобы получилась группа.

5.4.   Докажите, что если в группе G

а)   выполняется тождество , то G коммутативна;

б) не более четырех элементов, то G коммутативна.

5.5.  Докажите, что следующие группы изоморфны:

а)   ( 2Z, + )   и   ( 3Z, + );

б)   ( R, + )   и   ;

в)     и  ;

г)   симметрическая группа  и группа из задачи 5.2 л);

д)   знакопеременная группа  и группа собственных движений тетраэдра;

е)   симметрическая группа  и группа собственных движений куба;

ж)   группа из задачи 5.1 ж) и группа из задачи 5.1 з).

5.6. Какое из следующих числовых множеств образует кольцо (поле) относительно обычных операций сложения и умножения:

а)  множество nZ– целых чисел, кратных n;

б)  множество рациональных чисел, в несократимой записи которых знаменатели являются  степенями фиксированного простого числа p;

в)  множество действительных чисел вида , где  ;

г)  множество комплексных чисел вида , где  ;

д)  множество комплексных чисел вида , где  ?

5.7.  Какие из указанных множеств матриц образуют кольцо (поле) относительно обычных операций сложения и умножения матриц:

а)  множество вещественных симметрических матриц порядка n;

б)  множество вещественных ортогональных матриц порядка n;

в)  множество верхних треугольных матриц порядка n;

г)  множество квадратных матриц порядка n, у которых последняя строчка -- нулевая;

д) множество вещественных матриц вида  ?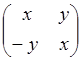

5.8.  Какие из следующих множеств образуют кольцо (поле) относительно указанных операций:

а) множество функций вещественного переменного, непрерывных на отрезке , относительно обычных операций сложения и умножения;

б) множество функций вида , относительно обычной операции сложения и  и композиции (в качестве умножения);

в)  множество монотонных функций вещественного переменного, непрерывных на отрезке , относительно обычных операций сложения и умножения;

г) множество функций  вещественного переменного, обладающих свойством , относительно обычных операций сложения и умножения;

д)  множество многочленов с действительными коэффициентами, относительно обычных операций сложения и умножения;

е)  множество многочленов четных степеней с действительными коэффициентами, относительно обычных операций сложения и умножения;

ж)  множество всех подмножеств универсального множества U относительно операций разностная сумма и пересечение множеств;

з)  множество всех подмножеств универсального множества U относительно операций объединение и пересечение множеств;

5.10.  Докажите, что поле из задачи 5.7 д) изоморфно полю комплексных чисел C.

5.11. Докажите, что множество, что поле   изоморфно полю   ,  где   обозначает операцию .

5.12. Докажите, что поле  с операциями, определенными следующим образом:   и  , изоморфно полю комплексных чисел Cс обычными операциями сложения и умножения.