Билет 21
1.Формула Остроградского-Гаусса. Формула Остроградского связывает поток через замкнутую поверхность S с интегралом по обьему, ограниченной этой поверхностью.
Орпд: Поверхносная область V (тело) называется поверхносно односвязной если всякую замкнутую кривую LÎ V можно стянуть в точку не выходя за пределы области V.
ТЕОРЕМА: Пусть векторная ф-ция F(М)
непрерывная вместе с частными производными : 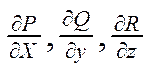 в
точках тела V вкл. его границу s, где s – кусочно гладкая замкнутоя поверхность. Тогда поверхносный
интеграл 2-го рода (поток) по внешней стороне поверхности равен 3-му интегралу
пр-ной области V:
в
точках тела V вкл. его границу s, где s – кусочно гладкая замкнутоя поверхность. Тогда поверхносный
интеграл 2-го рода (поток) по внешней стороне поверхности равен 3-му интегралу
пр-ной области V:
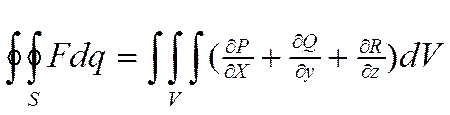
2.
Вычислить
криволинейный интеграл: ![]() , где
, где 
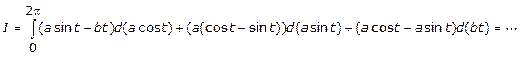 успехов, пацан!
успехов, пацан!
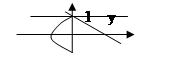 3.
3.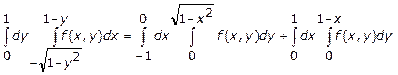
4. Уравнения, разрешенные относительно производной порядка n: ![]() .
.
5. Метод Лагранжа решения линейных неоднородных ДУ.
Будем искать решения лин. неод. ур-я в виде:y’+p(x)y=g(x), y=C(x)(e^(-интеграл от p(x)dx)), где С – функция C(x);y’=C(x)(e^(- интеграл от p(x)dx)) – C(x)p(x)(e^(-интеграл от p(x)dx)) =>C’(x)(e^(- интеграл от p(x)dx))=g(x)
Y(x)=e^(-интеграл от p(x)dx)*(C+интеграл от g(x)(e^(интеграл от p(x)dx))dx
6.Решить:
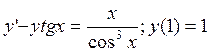 .
.
![]()
![]()
![]()
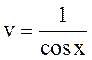
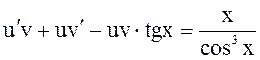
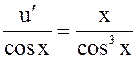
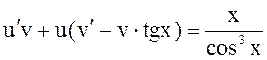
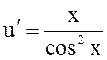
![]()
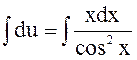
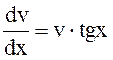
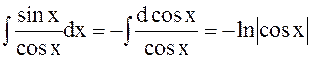
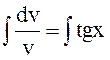
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.