Решение линейных неоднородных ДУ методом Лагранжа. Вычисление криволинейного интеграла II-го рода. Формула Стокса

Билет 16

1.Решение линейных неоднородных ДУ методом Лагранжа.

2.

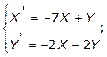
дифференцируем 1-ое уравнение :

= -7+

Y^’=+7X    ;   Y=X^’+ 7X

X^’’+7X = -2X -5Y

X^’’+7X = -2X -5( +7X );

X^’’+12X+37=0

+12+37=0

= -6 +/- ( i)

X=(  +   )

X^’=-6 (+) + ( - +  )

                              Т.К  Y= X^’ + 7X, ТО

Y= -6e^-6t ( +С₂ sint ) +e^-6t (- + )   + 7( C₁cost  +  C₂ sint )

ОТВЕТ:     X= ( e^-6t  (C₁cost + C₂sint)

                Y= ( C₁(cost – sint) +  C₂ ( cost  + sint))

3. Вычисление криволинейного интеграла II-го рода.

1)  Кривая – пространственная, задана параметрически 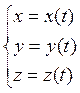 , , то КРИ-2 вычисляется по формуле:

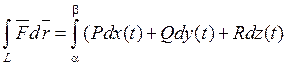
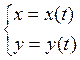2)  – плоская кривая: , , то

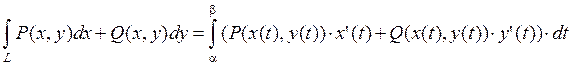
3) – плоская кривая в декартовых координатах:  , .

Переходим к параметрическим , .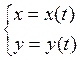

.

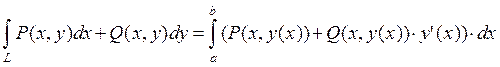4. F(x)=(x - 1)sin2x  –  x²e^2x + 5K_1,2=2            K_3,4=+2i

Y_=C₁ e^2x + C₂ xe^2x + ( C₁cos2x + C₂sin2x)

Y*=x²((Ax+B)cos2x + (A₁x + B₁)sin2x) + x(A₂ x +B₂ x+C₂ x) e^2x + A₃

5. Формула Стокса. Рассмотрим кусочно-гладкую поверхность S ограниченную замкнутым контуром L. Выберем нормаль n и направление обхода контура l так, чтобы со стороны нормали обход выполнялся против часовой стрелки. Пусть в точках поверхности S, включая границу l, определена непрерывная векторная функция F(H)=P(H)+Q(H)+R(H), причем P,Q,R имеют также требуемые непрерывные частные производные, тогда верна теорема: Интеграл 2-го рода по контуру L выражается через поток сквозь поверхность S по формуле Стокса: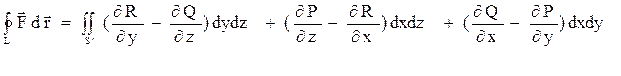

6. - ydx + xdx =((-3at²/(1+t³))*d(3at / (1+t³)))+(( 3at / (1+t³))*d(3at / (1+t)³))=

=-9a²((t²(1+t³-3t³) / (1+t³)( 1+t³)²)dt )+ 9a²(t(2t(1+t³)-(3t²)) / (1+t³)( 1+t³) ²)dt=

=-9a²(((-2t⁵+t²) / (1+t³)³)dt) + 9a²  ((- t⁵+2t²) / (1+t³)³)dt = =

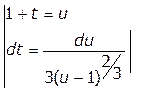=9a²(((u-1)^2/3(2u-2-1)du) /3u³(u-1)^2/3) - 9a²((u-1)^2/3(u-1-2)du) / 3u³(u-1)^2/3 =

==3a²((2u-3)dy / u³ )-3a²(u-3)du / u³= (-6a²)*1/u+(9a²)1/2u²+(3a²) *1/u-

-(9a²)1/2u²= -3a² + 6a² + (9a²/8) - (9a²/2) + (3a²/2) - 3a² (9a²/8) +(9a²/2) = 3a²/2