Механизмы двигателей внутреннего сгорания. Рычажный механизм. Зубчатый механизм. Кулачковый механизм

Техническое задание

Исходные данные

Механизмы ДВС состоят из рычажных,  зубчатых, кулачковых механизмов.

Рычажный механизм ДВС состоит из кривошипа 1, шатунов 2 и 4, ползунов 3 и 5.

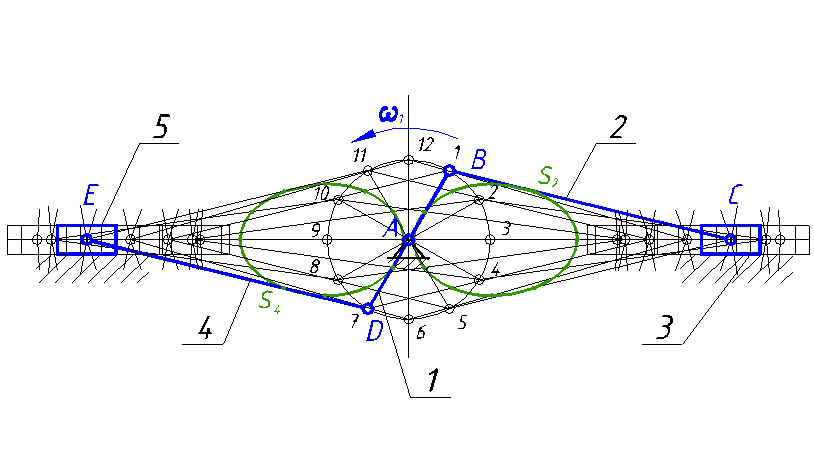       Рисунок 1 - Кинематическая схема рычажного механизма ДВС

Индикаторная диаграмма – графическая зависимость давления в цилиндре двигателя внутреннего сгорания или компрессора от положения поршня. В механизме ДВС четырехтактный цикл работы в каждом цилиндре осуществляется за 2 оборота кривошипа и содержит такты: всасывание (кривая a-b), сжатие b-c, расширение (рабочий ход) c-d-e и выпуск e-a.

В цилиндре Е происходит такт “расширение”, т.е. сила, действующая на поршень, направлена по движению поршня и является движущей. В остальных тактах действуют силы сопротивления, направленные против движения. Для каждого положения кривошипа давление в цилиндре определяют путем сноса точки положения поршня на соответствующую линию индикаторной диаграммы.

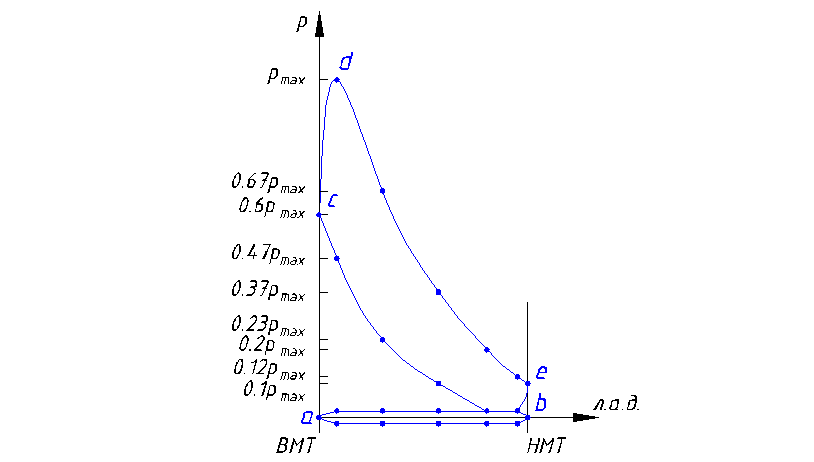            Рисунок 2 – Индикаторная диаграмма

В цилиндре С происходит такт “всасывание” и воздух всасывается из атмосферы в цилиндр. При всасывании давление ниже атмосферного.

Угловая скорость кривошипа: ω₁ = 125 рад/с.

Длины звеньев АВ и АD: l_AB = l_AD = 0,095 м.

Длины звеньев BC и DE: l_BC = l_DE = 0,35 м.

Центр масс звеньев BC и DE: l_BS2 = l_DS4 = 0,3 l_BC .

Диаметр цилиндра: d_ц = 100 мм.

Масса кривошипа: m₁ = 27 кг.

Масса шатунов 2 и 4: m₂ = m₄ = 3,5 кг.

Масса ползунов 3 и 5: m₃ = m₅ = 1,7 кг.

Момент инерции центров масс шатунов: I_S2 = I_S4 = 0,015 кг·м².

Максимальное давление: p_max = 2,3 МПа.

Коэффициент неравномерности: δ = 0,008

Зубчатый механизм

Движение коленчатого вала 1 передается на зубчатый механизм, состоящий из планетарной ступени 1-Н с модулем , и простой 4-5 с модулем

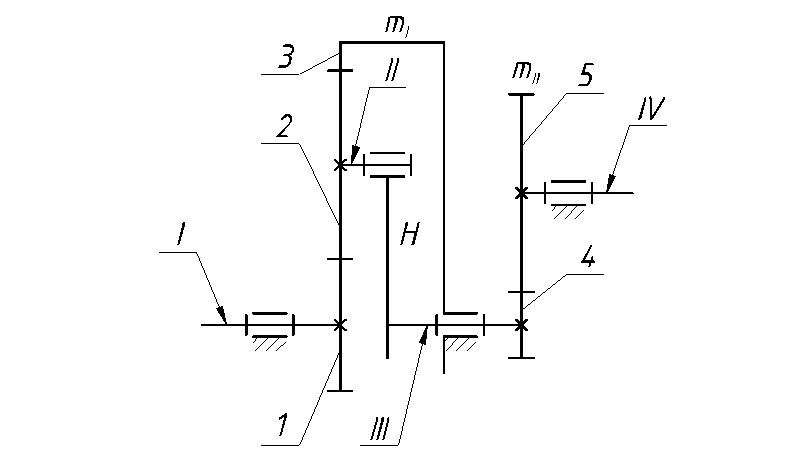
Рисунок 3 - Кинематическая схема сложного зубчатого механизма.

Исходные данные:

Число зубьев колеса 4: z₄ = 12;

Число зубьев шестерни 5: z₅ = 28;

Передаточное отношение планетарной передачи: i³_1H = 4,2;

Модуль планетарной ступени: m_I  = 6;

Модуль простой ступени: m_II = 8.

Передаточное отношение простой ступени:

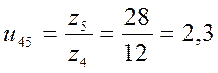
Зубчатая передача 4-5 проектируется со смещением.

Цели смещения: вписывание в стандартное межосевое расстояние, повышение износостойкости, изгибной прочности.

Кулачковый механизм

Кулачковый механизм с вращающимся толкателем состоит из кулачка 1, ролика 2 и толкателя 3.

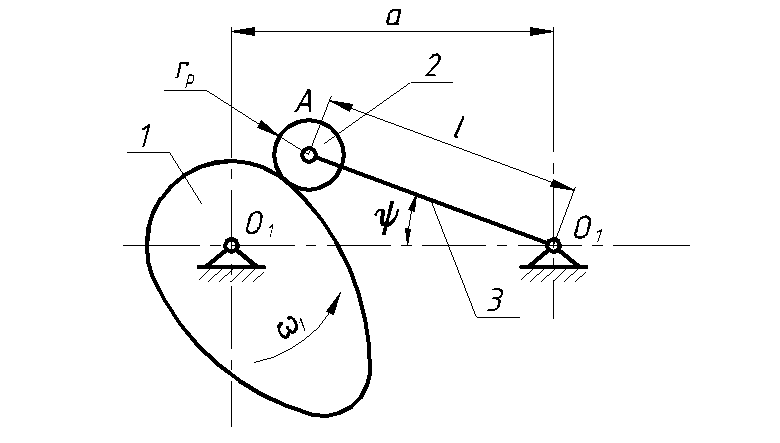
Рисунок 4 - Схема кулачкового механизма.

Исходные данные:

Вариант:  А211.

Закон движения толкателя:  синусоидальный.

Рисунок 5 – Закон движения толкателя

Движение толкателя: вращательное.

Фазовые углы: φ_у = 72˚;  φ_д = 108˚; φ_с = 72˚; φ_б = 108˚;

Угловой шаг: ∆φ = 12˚;

Максимальное угловое перемещение: ψ_max = 15˚;

Длинна коромысла: l = 80 мм

Радиус ролика: r_р = 15 мм;

Допускаемые углы давления на фазе сближения: = 30˚;

Допускаемые углы давления на фазе удаления: = 45˚.

1. Структурный кинематический и кинетостатический анализ плоского рычажного механизма

                 1.1. Структурный анализ механизма

Число степеней свободы по формуле Чебышева:

,                                   (1)

где  n - число подвижных звеньев, n = 5;

p₁ - число низших кинематических пар, p₁ = 7

p₂ - число выcших кинематических пар, p₂ = 0.

Рычажный механизм имеет одно начальное звено.

Отсоединяем группы Асcура (диады) с n = 2, p = 3.   

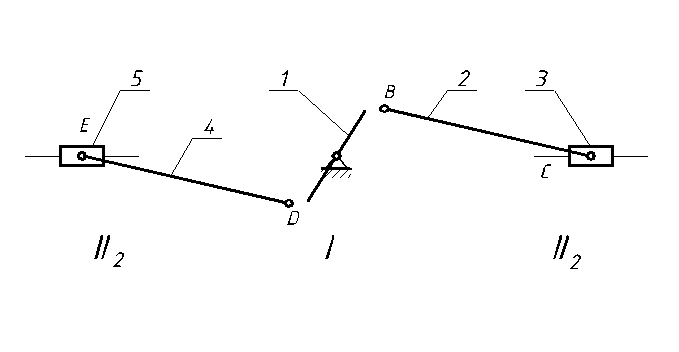
Рисунок 6 - Группы Ассура

Формула строения механизма:

                        .

Данный механизм относиться ко второму классу.

1.2. План положений

Масштаб плана положений:

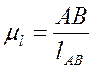,                                             (2)

где AB – длина отрезка, изображающего длину звена; l_AB – длина звена АВ.

.

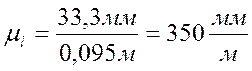Длины отрезков, отображающих длины звеньев:

.

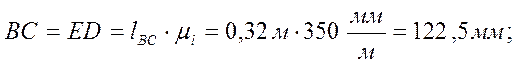
Вычерчиваем окружность радиуса AB и делим ее на 12 частей. Из точек В, длиной ВС на направляющей откладываем засечки С. Соединяем получившиеся точки С с точками В. Из точек В на шатунах ВС длиной BS₂ откладываем засечки S₂ . Соединяем полученные точки S₂ и получаем шатунные кривые. Аналогичные операции производим для шатуна DE.

                          1.3. План скоростей

Построение планов решает задачу графического определения искомых параметров.

В методе планов используют принцип известный из теоретической механике, в соответствии с которым движение точки любого звена подчиняется следующему  векторному уравнению:

,                                       (3)

где   - абсолютная скорость искомой точки;

-переносная скорость;

-относительная скорость.

Первую систему составляем для группы Ассура 2-3:

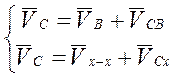  .                                    (4)

В первом уравнение системы скорость V_B направлена перпендикулярно звену АВ,  V_CB - перпендикулярно звену СВ, а скорость V_C вдоль направляющей х-х.

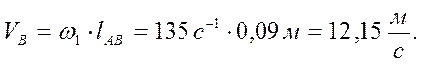                  (5)

По заданной скорости V_B выбираем масштаб планов скоростей:

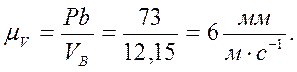                             (6)