План скоростей строим в
масштабе μV в
следующем порядке: выбираем положение полюса p плана скоростей. Из этого полюса перпендикулярно звену АВ
проводим отрезок Pb. Затем через
полюс проводим направление скорости VC . Из точки b перпендикулярно
звену ВС проводим направление скорости VB и получаем точку с. На векторе bc находим точку S2 исходя из того, что S2b =
0,3bc. Через p и S2 проводим вектор, который обозначает
скорость VS2. Из плана скоростей находим действительное значение
скоростей путем деления величины векторов на масштаб ![]()
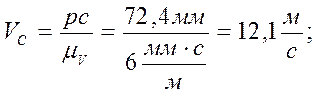 (7)
(7)
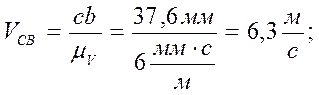 (8)
(8)
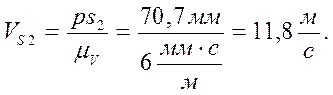 (9)
(9)
Зная скорость ![]() находим
угловую скорость звена 2:
находим
угловую скорость звена 2:
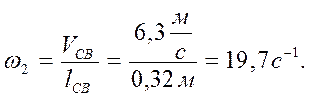 (10)
(10)
План скоростей для группы Асура 4-5 строится аналогично группе Асура 2-3.
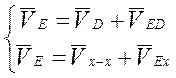 (11)
(11)
Находим скорости из плана:
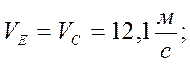
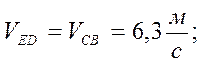
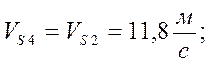
![]()
1.4. План ускорений
Векторное уравнение для построения плана ускорений имеет следующий вид:
![]() (12)
(12)
где ![]() – полное ускорение
искомой точки;
– полное ускорение
искомой точки;
![]() -переносное ускорение;
-переносное ускорение;
![]() - ускорение Кориолиса;
- ускорение Кориолиса;
![]() -относительное
ускорение.
-относительное
ускорение.
![]() (13)
(13)
Во вращательной кинематической паре ускорение Кориолиса равно нулю.
Система векторных уравнений группы Асура 2-3:
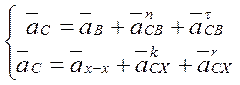 .
(14)
.
(14)
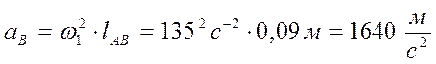 , (15)
, (15)
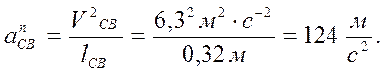 (16)
(16)
Выбираем масштаб плана ускорений ![]()
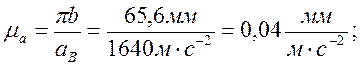 (17)
(17)
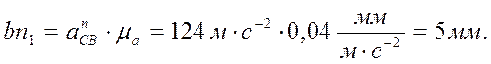 (18)
(18)
План ускорений строим в
масштабе μa в
следующем порядке: выбираем положение полюса π плана скоростей. Из этого полюса
проводим вектор длиной πb
(направлен к оси вращения кривошипа). Затем из точки b строим вектор bn1
который направлен
вдоль шатуна. Через точку n1 проводим прямую перпендикулярно bn1 . Через полюс проводим направление ускорения точки С,
на пересечении получаем точку с. Строим вектор n1c. На
векторе n1c находим точку S2 , исходя из того, что S2b = 0,3bc. Из
плана ускорений находим действительное значение ускорений путем деления
величины векторов на масштаб ![]()
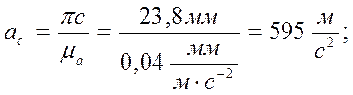 (19)
(19)
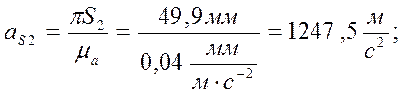 (20)
(20)
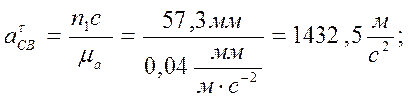 (21)
(21)
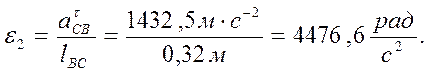 (22)
(22)
План ускорений для группы Ассура 4-5 строится аналогично группе Ассура 2-3.
Система векторных уравнений группы Асура 4-5:
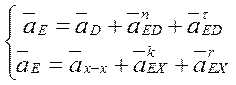 . (23)
. (23)
Находим ускорения из плана:
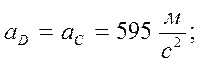
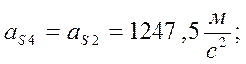
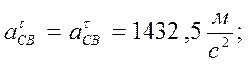
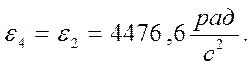
1.5. Кинематические диаграммы
Диаграмму перемещений SC = f(t) строим в масштабе μS = μl = 370 мм/м. Текущие значения перемещений отсчитываем от крайнего левого положения ползуна с плана положений механизма.
Масштаб времени:
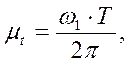 (24)
(24)
где T - отрезок на оси абсцисс, соответствующий времени одного оборота кривошипа; T = 180 мм.
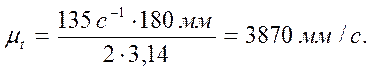
Диаграмму скорости VC = f(t) строим методом графического дифференцирования, располагая ее под диаграммой SC = f(t). На продолжении оси абсцисс диаграммы VC = f(t) влево от начала координат откладываем полюсное расстояние Op1 = H1 = 40 мм. Далее в соответствии с методом секущих из точки p1 проводим лучи p11’, p12’… параллельно хордам кривой SC = f(t) соответствующих участков. Эти лучи отсекают на оси ординат отрезки, пропорциональные средней скорости VC на соответствующем участке диаграммы. Полученные отрезки откладываем на средних ординатах участков. Соединяя полученные точки плавной кривой, получаем диаграмму скорости. VC = f(t) Масштаб диаграммы скорости:
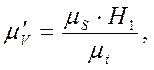 (25)
(25)
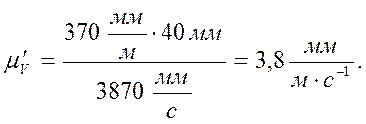
По диаграмме скорости VC = f(t) аналогично строим диаграмму ускорения aC = f(t). От начала координат диаграммы VC = f(t) откладываем отрезок Op2 = H2 = 40 мм. Хорды поводим на участках, соответствующих диаграмме перемещений.
Масштаб диаграммы ускорения
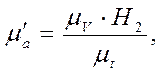 (26)
(26)
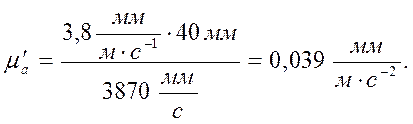
1.6. Аналитический метод кинематического анализа
1.6.1. Исходные данные
Угловая скорость кривошипа: ω1 = 135 рад/с.
Длины звеньев АВ и АD: lAB = lAD = 0,09 м.
Длины звеньев BC и DE: lBC = lDE = 0,32 м.
Центр масс звеньев BC и DE: lBS2 = lDS4 = 0,3 lBC = 0,096 м.
Угол поворота кривошипа: φ1 = 30˚ … 360˚, 30˚.
1.6.2. Алгоритм расчета
Расчетная схема кинематической цепи приведена на рис. 5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.