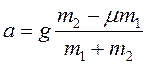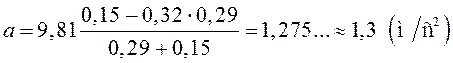Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 9

;                                  

.

Ответ: тела будут двигаться с ускорением .

2.5.  Движение под действием переменных сил

Если силы, действующие на тело, при его движении изменяются с течением времени, то ускорение, с которым движется тело, не будет оставаться постоянным. Это обстоятельство делает невозможным использование формул кинематики равноускоренного движения и требует применения дифференциального и интегрального исчисления при решении задач такого типа.

Задача 11. Водный мотоцикл массой 160 кг (без водителя) движется по спокойной воде. После падения водителя на крутом вираже и автоматической остановки двигателя скорость мотоцикла при его дальнейшем движении по прямой за 4,5 с уменьшилась в 10 раз. Считая силу сопротивления движению пропорциональной скорости (), найти коэффициент сопротивления .

Решение.

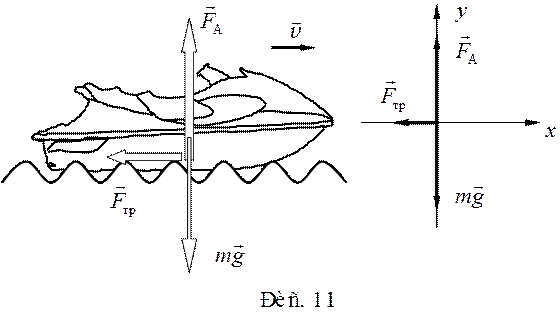Движение вод-ного мотоцикла пос-ле остановки двигателя происходит под действием трех сил: силы тяжести, направленной вертикально вниз, силы Архимеда, направленной  вверх, и силы сопротивления, направленной против скорости. На основании второго закона Ньютона запишем уравнение движения:

.                                

Выберем ось Ox вдоль направления движения. Тогда для этой оси уравнение можно переписать с учетом того, что проекции силы тяжести и силы Архимеда на горизонтальную ось равны нулю, а проекция силы сопротивления :

.                                     

Из уравнения видно, что ускорение, с которым движется водный мотоцикл, не остается постоянным с течением времени, а изменяется вместе с изменением скорости. По определению для ускорения при одномерном движении и произвольном характере зависимости ускорения от времени можно записать:

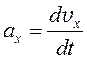
(именно поэтому в уравнении не взяты проекции скорости и ускорения).

Подставляя формулу в уравнение , получим дифференциальное уравнение с разделяющимися переменными, в котором неизвестной является функция скорости от времени:

.                                   

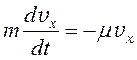Разделим переменные и проинтегрируем обе части уравнения , полагая, что секундомер был включен в момент выключения двигателя:

.                                  

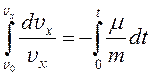С учетом формулы Ньютона-Лейбница и правил потенцирования, получим:

.                                    

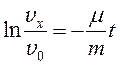Если необходимо получить зависимость скорости от времени, то следует взять экспоненту от обеих частей выражения и применить к левой части основное логарифмическое тождество. В данной задаче искомую величину выразим непосредственно из формулы :

;                                     

.

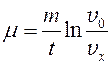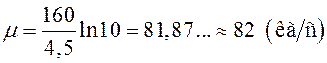Ответ: коэффициент сопротивления движению .

2.6.  Движение тел с изменяющейся массой

При описании движения тел, масса которых изменяется в процессе движения (например, из движущейся цистерны вытекает вода), нельзя применить второй закон Ньютона в привычной (интегральной) форме, поскольку он справедлив только для тел, масса которых остается неизменной. Ниже приведен пример решения задачи, в которой уравнение движения записывается на основании второго закона Ньютона в дифференциальной форме, так как масса движущейся ракеты быстро убывает вследствие работы двигателей (в более общем случае уравнением движения таких тел является уравнение Мещерского).

Задача 12. При выводе на орбиту космического корабля «Буран» массой 100 т было сожжено 2000 т топлива. Найти скорость взлетающей ракеты через 3 мин после старта, полагая, что 1) первые несколько минут корабль взлетает вертикально вверх; 2) 90 % топлива было израсходовано двигателями первой ступени ракеты-носителя «Энергия» за 6 мин их работы; 3) расход топлива и сила тяги двигателей за это время оставались постоянными; 4) сила тяги двигателей в полтора раза превышает стартовый вес ракеты.