Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 10

При работе ракетных двигателей вследствие быстрого сгорания топлива изменяются масса взлетающей ракеты и сила тяжести, действующая на ракету со стороны Земли. Уравнением движения ракеты будет являться основной закон динамики материальной точки (частицы) в дифференциальной форме:

.                                    

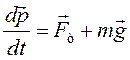Выберем ось Ox вертикально вверх и возьмем проекции векторов на эту ось, получим:

.                                    

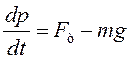Поскольку расход топлива постоянен, то масса ракеты линейно уменьшается с течением времени по закону:

.                                     

Подставляя формулу в уравнение , получим дифференциальное уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем обе части полученного уравнения:

.                        

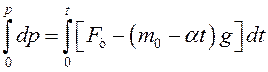Вычислим интегралы и по формуле Ньютона-Лейбница получим:

.                           

Поскольку за время  работы двигателей первой ступени сгорает  топлива, то расход топлива найдем по формуле:

.                              

Модуль импульса взлетающей ракеты, очевидно, определяется формулой:

.                              

Подставляя формулы и в выражение и учитывая, что , после элементарных преобразований получим:

                          

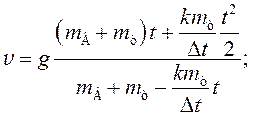
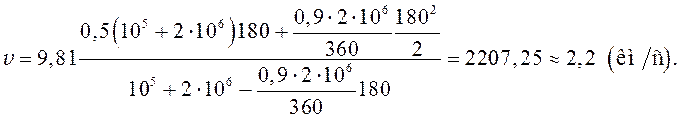
Ответ: ракета достигнет скорости

Библиографический список

1. Трофимова Т. И. Курс физики / Т. И. Трофимова. М., 1997. 542 с.

2. Детлаф А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. М., 2000. 718 с.

3. Савельев И. В. Курс общей физики / И. В. Савельев. М., 1989. Т. 1. 352 с.

ПРИЛОЖЕНИЕ 1

Проекция вектора на ось

При работе с векторами удобно придерживаться следующих обозначений:  – вектор (в учебниках обозначается жирной буквой без стрелочки);

a,  – модуль вектора (длина вектора, числовое значение вектора);

 – проекция вектора  на ось Ох (компонента вектора);

 – составляющая вектора  по оси Ох.

Рис. П.1.1

Проекцией вектора  на ось Ох называется алгебраическая величина, определяемая выражением: , где a – модуль вектора; α – угол между вектором и осью (рис. П.1.1). Составляющая  вектора  нап-равлена вдоль оси Ох в ту же сторону, что и вектор , а проекции вектора  и его составляющей  на эту ось равны (см. рис. П.1.1).

Пример. Пусть в некоторый момент времени угол между вектором ско-рости тела и осью Ох равен 30^о, а длина вектора скорости равна 2,8 м/с. Найти проекции вектора скорости на координатные оси Ох и Оу.

Рис. П.1.2

Дано: v  = 2,8 м/с, α1 = 30о vx,vy  – ? Решение. vx = v cos α1; vx = 2,8 cos 30о = 2,4 (м/с); vy = v cos α2; vy = 2,8 cos (90о + 30о) =  – 1,4 (м/с).

Обратите внимание: проекции вектора на разные оси могут быть разными, а модуль вектора не зависит от выбора осей.

Таблица П.1

Пять частных случаев вычисления проекции

1.  Вектор направлен вдоль оси.	, Проекция вектора равна модулю.
2.  Вектор перпендикулярен оси.	, Проекция вектора равна нулю.
3.  Вектор направлен против оси.	, Проекция вектора равна «минус модуль».
4.  Острый угол между вектором и осью.	, , Проекция вектора положительна.
5.  Тупой угол между вектором и осью.	, , , Проекция вектора отрицательна.

Обратите внимание: если составляющая вектора направлена в ту же сторону, что и ось, то проекция такого вектора положительна; если составляющая направлена против оси, то проекция вектора отрицательна.

Учебное издание

КУРМАНОВ  Рамиль Султангареевич,

ЛИТНЕВСКИЙ  Леонид Аркадьевич

КИНЕМАТИКА  И  ДИНАМИКА  ЧАСТИЦ

В  ПРИМЕРАХ  РЕШЕНИЯ  ЗАДАЧ

––––––––––––––––––

Редактор Т. С. Паршикова

***

Подписано в печать     .05.2009. Формат 60 × 84 ¹/₁₆.

Плоская печать. Бумага офсетная. Усл. печ. л. 2,1. Уч.-изд. л. 2,3.

Тираж 800 экз. Заказ         .

**

Редакционно-издательский отдел ОмГУПСа

Типография ОмГУПСа

*

644046, г. Омск, пр. Маркса, 35