Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 2

1.  КИНЕМАТИКА

Решение кинематических задач по механике опирается на знание нескольких формул кинематики и умение пользоваться векторной алгеброй и дифференциальным и интегральным исчислением. При рассмотрении приведенных ниже примеров решения задач необходимо обратить внимание на возможности, которые открываются при применении векторной алгебры.

Векторная алгебра, одним из создателей которой в ее современной форме был американский физик-теоретик Дж. У. Гиббс (1839 – 1903), является мощным универсальным инструментом решения задач по разделу «Кинематика».

1.1.  Одномерное равноускоренное движение

Равноускоренным называется такое движение частиц (небольших тел, «материальных точек»), при котором они движутся с постоянным ускорением, т. е.  . Напомним, что вектор считается неизменным, если с течением времени не изменяются ни его длина (модуль, числовое значение), ни его направление в пространстве. При этом не обязательно, чтобы скорость тела возрастала. Так, при торможении автомобиля перед светофором с постоянным ускорением (можно было бы сказать «замедлением», но в физике такой термин не используется) его движение также считается равноускоренным.

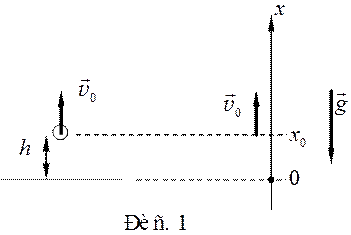Задача 1. Небольшой металлический шарик подброшен вертикально вверх с начальной скоростью 12 м/с с высоты 1,36 м над уровнем пола. Найти скорость, положение и перемещение шарика к моменту времени 1,4 с после начала движения. Сопротивлением воздуха пренебречь.

В задачах такого типа не рассматривается процесс разгона шарика до заданной начальной скорости. Всё, что произошло с шариком до момента включения секундомера (t₀ = 0), заключено в заданной начальной скорости и начальном положении рассматриваемого тела.

Небольшие тяжелые тела вблизи поверхности Земли движутся с постоянным ускорением, равным ускорению свободного падения, если сопротивлением воздуха можно пренебречь. Для равноускоренного движения справедливы формулы кинематики:

;                                     

.                                        

Векторным формулам и при движении тела вдоль одной прямой (такое движение является одномерным) соответствуют аналогичные выражения, записанные для проекций векторов (обычно после приобретения навыков работы с векторами эти формулы подразумевают, но не записывают):

;                                   

.                                      

Возьмем проекции векторов на координатную ось. Под словами «взять проекцию» понимаем: «выразить проекцию через модуль вектора и косинус угла между вектором и осью» в соответствии с определением проекции произвольного вектора :

.                                       

Поскольку направления векторов  и  неизвестны, взять проекции этих векторов невозможно. Итак (рис. 1), получим:

;                                    

;

;                                       

.

Зная, что проекция перемещения на координатную ось равна разности координат начального и конечного положений тела, найдем положение (координату) шарика в заданный момент времени:

;                                        

.

Проанализируем полученные результаты. Проекция перемещения оказалась положительной, значит, вектор перемещения направлен в ту же сторону, что и ось координат, и шарик в заданный момент времени оказался выше начального положения. Проекция скорости шарика оказалась отрицательной, следовательно, в этот момент времени он уже летел вниз, несколькими долями секунды раньше достигнув наибольшей высоты.

Обратите внимание на правила округления результатов расчетов. В условии задачи значения величин заданы с двумя и тремя значащими цифрами (положение запятой не имеет значения), значит, округлять результаты расчетов надо также до двух значащих цифр. Однако в промежуточных расчетах (например, число 7,186, полученное при вычислении по формуле , было использовано при расчетах по формуле ) необходимо оставить на несколько (одну, две) значащих цифр больше.