Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 4

Дано: R = 6,3 м l = v = const t = 1,2 с	Решение.
– ?

При движении тела по окружности его ускорение можно разложить на две составляющие ускорения – тангенциальное и нормальное:

.                                      

Если модуль скорости остается неизменным, то тангенциальное ускорение равно нулю. Следовательно, в этой задаче ускорение, с которым движется тело, является нормальным:

.                                    

Скорость движения модели самолета найдем, учитывая, что при движении тела с постоянной по модулю скоростью путь (не перемещение), пройденный телом, можно вычислить по формуле:

.                                          

Подставляя в формулу путь, равный третьей части длины окружнос-ти, получим:

.                                       

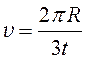Тогда нормальное ускорение

.                                      

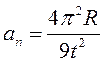Модуль нормального ускорения, безусловно, не изменяется при движении тела, однако вектор нормального ускорения поворачивается и, следовательно, не остается постоянным. Тогда изменение ускорения равно модулю разности векторов ускорений, взятых в два разных момента времени:

.                         

Из формулы следует, что для определения разности векторов надо ко второму вектору прибавить вектор, противоположный первому. Из рис. 3 видно, что длина такого вектора может быть найдена по теореме косинусов:

;       

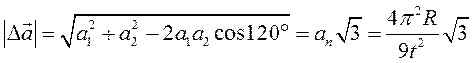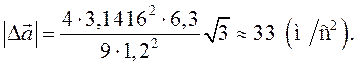
Направление вектора  показано на рис. 3.

Ответ: модуль изменения ускорения равен 33 .

1.4.  Относительность движения

Задача 4. Два корабля движутся относительно острова со скоростью 4,8 и 6,4 м/с под углом 30 и 60° к востоку от меридиана соответственно. С какой скоростью второй корабль движется относительно первого?

Дано:	Решение.
– ?

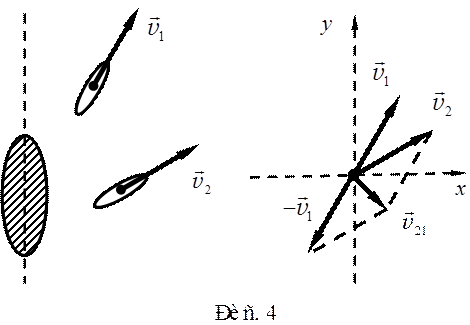
Для решения задачи воспользуемся формулой:

,                                      которая выражает принцип относительности движения и позволяет переходить от одной системы отсчета к другой. Тогда модуль относительной скорости

; 

Этот путь поиска численного ответа в задаче основан на рис. 4 и не поз-воляет непосредственно указать в количественном виде направление результирующего вектора относительной скорости.

Эту же задачу можно решить другим способом. Выразим из формулы неизвестную относительную скорость:

,                                      возьмем проекции известных векторов и получим:

;                       

;

;                      

.

Модуль относительной скорости, очевидно, равен квадратному корню из суммы квадратов проекций, и результат вычислений, безусловно, совпадет с результатом, полученным по формуле , в чем можно убедиться самостоятельно.

Преимущества второго способа заключаются в том, что, во-первых, его можно применять для любого количества складываемых (или вычитаемых) векторов (теорема косинусов позволяет работать только с парой векторов), а во-вторых, можно явно указать направление результирующего вектора, вычислив, например, угол между результирующим вектором и осью Ox:

;                                      

.

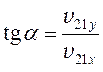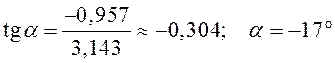Отрицательное значение угла α означает, что угол нужно отложить вниз от оси Ox (по ходу часовой стрелки).

Ответ: скорость относительного движения кораблей равна 3,3  и направлена под углом 17° к оси Ox на юго-восток.

1.5.  Обратная задача механики

Обратная задача механики заключается в определении характеристик движения (скорости, ускорения и т. д.) по известной зависимости радиуса-вектора от времени. В общем случае задача решается на основе дифференциального исчисления и векторного анализа, другими словами, для решения обратной задачи механики необходимо уметь находить производные функций и знать правила работы с векторными величинами. Решение задачи 5 можно рассматривать как пример применения определений скорости, ускорения, траектории и других понятий кинематики.