Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 5

Задача 5. Частица движется так, что зависимость ее координат от времени описывается выражениями:  и , где , . Найти зависимость скорости и ускорения частицы от времени, ее тангенциальное и нормальное ускорение через 3,5 с после начала движения, а также радиус кривизны траектории в этот же момент времени и уравнение траектории.

Решение.

Знание зависимости координат движущегося тела от времени (эти функции часто называют законом движения) эквивалентно знанию радиуса-вектора:

  .

По определению скоростью тела является производная от радиуса-вектора по времени, тогда с учетом правил дифференцирования и таблицы             производных получим:

.               

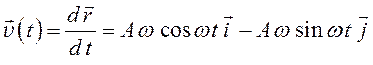Очевидно, что в формуле сомножители перед ортами декартовых осей координат (с учетом знака) есть проекции вектора скорости на координатные оси.

По определению ускорением тела является производная от вектора скорости по времени, тогда с учетом правил дифференцирования и таблицы производных получим:

.             

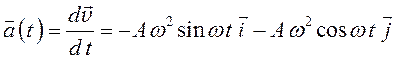По определению тангенциальным ускорением является производная от модуля скорости, а модуль скорости (как модуль любого вектора) есть квадратный корень из суммы квадратов проекций вектора на координатные оси:

.              

Оказалось, что модуль скорости не зависит от времени, и его производная по времени, очевидно, равна нулю в любой момент времени:

.                                     

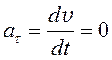Поскольку для полного, нормального и тангенциального ускорения справедлива формула

,                                       то в данной задаче полное ускорение частицы совпадает с ее нормальным ускорением и их в данный момент времени можно вычислить по формуле :

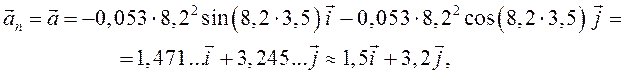     а модуль нормального и полного ускорения –

;        

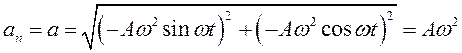Такой же ответ для модуля нормального ускорения в данный момент времени можно было бы получить, если извлечь квадратный корень из суммы квадратов значений проекций вектора ускорения, вычисленных по формуле , но в данной задаче интересно было увидеть в формуле , что модуль ускорения не зависит от времени.

Радиус кривизны траектории движения частицы найдем из формулы, известной из школьного курса физики:

.                                      

Поскольку в данной задаче ни модуль ускорения, ни модуль скорости не зависят от времени, то и радиус кривизны траектории также будет постоянной величиной:

;                      

.

Найдем уравнение траектории, по которой движется частица. По определению законы движения

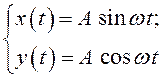
представляют собой уравнения траектории, заданной в параметрической форме. Чтобы получить уравнение траектории в явном виде, нужно в выражениях системы избавиться от времени как от параметра. Часто для этого достаточно выразить время из одного выражения и подставить его во второе, но в этой задаче удобнее возвести оба выражения системы в квадрат и сложить левые и правые части получившихся формул. С учетом основного тригонометрического тождества и выражения получим:

.  

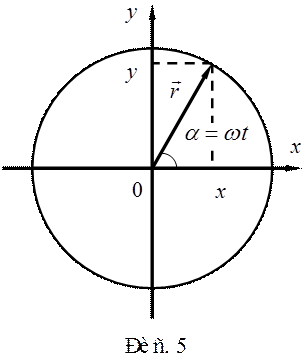
Конечно, далее можно выразить зависимость y от x в явном виде, однако в этой задаче в этом нет необходимости, так как из математики хорошо известно, что формула

есть уравнение окружности радиуса R (рис. 5 иллюстрирует полученный результат).

Ответ: частица движется по окружности радиуса 5,3 см с постоянной по модулю скоростью и нормальным ускорением 3,6 .

1.6.  Прямая задача механики

Прямая задача механики заключается в том, чтобы из известного уравнения движения (зависимости ускорения от времени) найти зависимость радиуса-вектора от времени. В задаче 5 было показано, что такая зависимость позволяет полностью описать движение.