Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 8

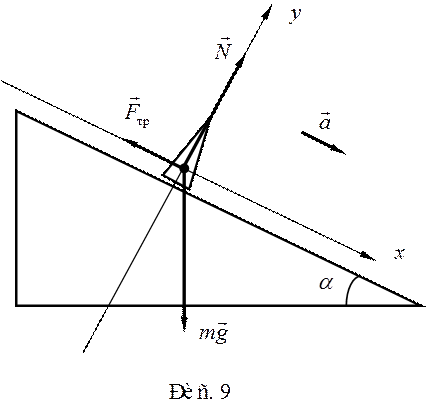
Движение лыжника по нак-лонной плоскости происходит под действием трех сил: силы тяжести, направленной вертикально вниз; силы реакции опоры, направленной перпендикулярно к опоре; силы трения скольжения, направленной против движения тела. Пренебрегая размерами лыжника по сравнению с длиной горки, на основании второго закона Ньютона запишем уравнение движения лыжника:

.                                

Выберем ось Ox вниз вдоль наклонной плоскости (рис. 9), а ось Oy – перпендикулярно наклонной плоскости вверх. Возьмем проекции векторов уравнения на выбранные координатные оси с учетом того, что ускорение направлено вдоль наклонной плоскости вниз, и добавим к ним выражение, определяющее силу трения скольжения. Получим систему уравнений:

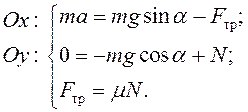
Решим систему уравнений относительно ускорения. Для этого из второго уравнения системы выразим силу реакции опоры и подставим полученную формулу в третье уравнение, а выражение для силы трения – в первое. После сокращения массы имеем формулу:

.                             

Ускорение не зависит от времени, значит, можно воспользоваться формулой кинематики равноускоренного движения, содержащей перемещение, ускорение и время:

.                                    

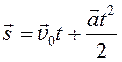С учетом того, что начальная скорость лыжника равна нулю, а модуль перемещения равен длине горки, выразим из формулы время и, подставляя в полученную формулу ускорение , получим:

;                            

.

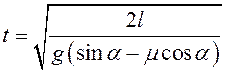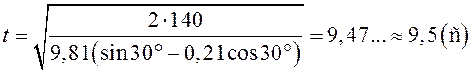Ответ: время спуска с горы 9,5 с.

2.4.  Движение связанных тел

При записи уравнений движения связанных тел необходимо иметь в виду, что второй закон Ньютона формулируется для тела (одного) массой m. Следовательно, при описании движения связанных тел уравнение движения должно быть записано для каждого тела в отдельности, а действие тел друг на друга определяется силой реакции опоры, натяжения нити и т. д.

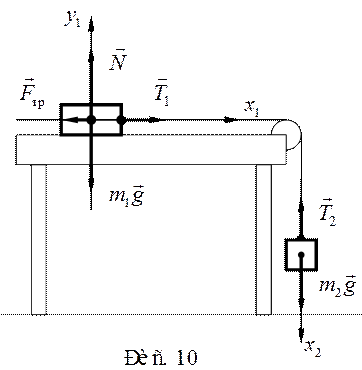
Задача 10. На столе находится небольшой деревянный брусок массой 290 г, к которому привязана нить, перекинутая через невесомый блок, закрепленный на краю стола. Ко второму концу нити привязан груз массой 150 г. С каким ускорением будут двигаться эти тела, если коэффициент трения дерева о стол равен 0,32?

На брусок (рис. 10), расположенный на столе, очевидно (см. задачу 8), действуют четыре силы: сила тяжести; сила реакции опоры; сила натяжения нити и сила трения. На груз, подвешенный на нити, перекинутой через блок, очевидно (см. задачу 7), действуют две силы: сила тяжести и сила натяжения нити. На основании второго закона Ньютона запишем уравнение движения для каждого из этих тел, полагая, что их размерами в данной задаче можно пренебречь:

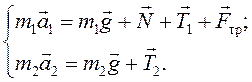
Координатные оси можно выбрать отдельно для каждого тела, поскольку после взятия проекций в формулах останутся только модули векторов (их длины), которые одинаковы во всех системах координат. Возьмем проекции векторов на координатные оси, добавим формулу для силы трения и получим:

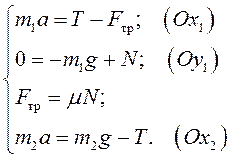
Поскольку движущиеся тела связаны, то за одинаковый промежуток времени они будут проходить одинаковое расстояние. Отсюда следует, что модули ускорений, с которыми движутся эти тела, одинаковы. Силы натяжения нити, приложенные к бруску и к грузу, возникают вследствие взаимодействия этих тел и по модулю равны друг другу (более подробное объяснение равенства модулей этих сил будет приведено при изучении вращательного движения тел).

Решение системы уравнений выполним в следующем порядке: из второго уравнения выразим силу реакции опоры и подставим в третье уравнение, а получившееся при этом выражение для силы трения подставим в первое:

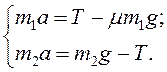
Сложим левые и правые части уравнений системы , при этом  в правой части полученного выражения взаимно уничтожится неизвестная сила натяжения нити, а затем выразим ускорение: