Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 6

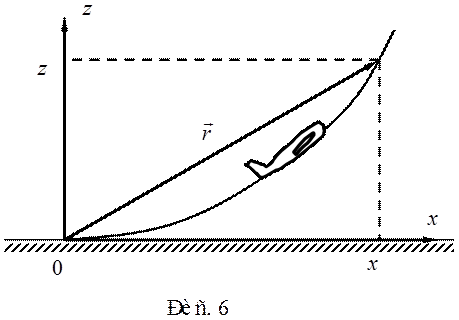
Задача 6. Небольшой одномоторный самолет первые  несколько десятков секунд после отрыва от взлетной полосы движется с ускорением , где ,  Начальным моментом времени считается момент отрыва от земли, причем к этому времени самолет набрал скорость . Найти положение самолета через 55 с после взлета. Считать, что ось Ox направлена вдоль взлетной полосы, а ось Oz – вертикально вверх. Начало координат выбрать в точке отрыва самолета от земли.

По определению ускорение в случае произвольного движения

.                                        

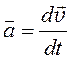Подставим в формулу функцию ускорения:

.                                

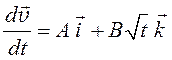В уравнении , тип которого – дифференциальное уравнение с разделяющимися переменными (этот тип уравнения решается наиболее просто), неизвестной является функция зависимости скорости от времени. Решается такое уравнение разделением переменных и интегрированием обеих частей полученного равенства:

.                           

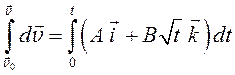Отсюда

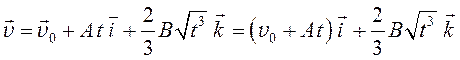,         так как начальная скорость была направлена только вдоль оси Ox.

Заметим, что уравнение можно решить и другими способами. Например, можно было записать неопределенный интеграл вместо определенного, а постоянную интегрирования найти из начальных условий, а также вмес-то интегрирования векторного уравнения можно было интегрировать два уравнения, записанные для каждой из проекций ускорения на координатные оси. Разумеется, что результат решения дифференциального уравнения во всех случаях будет одинаковым.

Аналогично найдем радиус-вектор. Воспользуемся теперь определением скорости произвольного движения:

.                                        

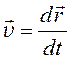Подставим в уравнение функцию , полученную выше:

.                        

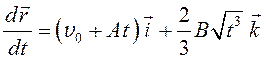Уравнение вновь является уравнением с разделяющимися переменными. Разделяя переменные и беря интегралы от обеих частей равенства, получим:

.                   

В формуле учтено, что в начальный момент времени самолет находился в начале координат (нулевой нижний предел первого интеграла).

После вычисления интегралов подставим численные значения и получим:

;                       

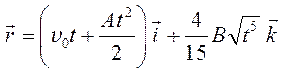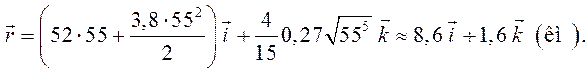
Ответ: за 55 с полета самолет удалился от точки взлета на 8,6 км по горизонтали и поднялся вверх на 1,6 км.

2.  ДИНАМИКА

Необходимая для решения прямой задачи механики зависимость ускорения от времени вытекает из уравнения динамики. Знание сил, действующих на тело, позволяет на основании второго закона Ньютона записать уравнение движения, связывающее действующие на тело силы и ускорение, с которым это тело будет двигаться. Если к этому уравнению добавить формулы кинематики, то получится система уравнений, решение которой позволяет найти значения неизвестных физических величин.

2.1.  Прямолинейное движение в вертикальном направлении

При разборе решения задачи 7 необходимо обратить внимание на то, какие силы, как правило, действуют на тело при таких условиях движения.

Задача 7. Подъемный механизм, поднимая ведро бетона массой 24 кг, действует на трос с силой 250 Н. Сколько времени будет длиться подъем этого груза на четвертый этаж (11 м)? Массой троса пренебречь.

Решение этой задачи состоит из двух взаимосвязанных частей: динамики и кинематики.

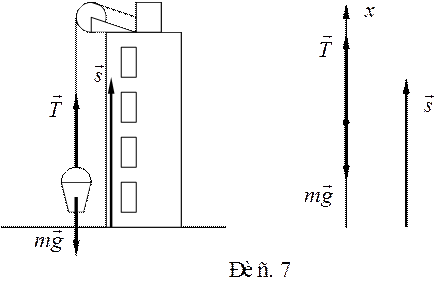
На тело, подвешенное на тросе, действуют две силы: сила натяжения, направленная вдоль троса, т. е. вертикально вверх (в данной задаче), и сила тяжести, направленная вертикально вниз (всегда). На основании второго закона Ньютона запишем уравнение движения груза:

.                                      

В данной задаче все векторы направлены вдоль одной прямой (рис. 7), поэтому можно ограничиться одной осью координат, направив ее, например, вертикально вверх. Возьмем проекции векторов выражения на эту ось и получим: