Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 7

,                                       отсюда определим ускорение, с которым будет подниматься груз:

.                                       

Поскольку ускорение оказалось постоянным, не зависящим от времени, то движение груза будет равноускоренным. Выберем формулу кинематики равноускоренного движения, содержащую перемещение, ускорение и время:

.                                      

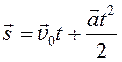Возьмем проекции на выбранную ось и, учитывая, что начальная скорость тела равна нулю, получим:

.                                          

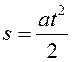Подставляя в выражение ускорение и выражая время, окончательно имеем:

;                                     

.

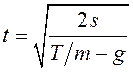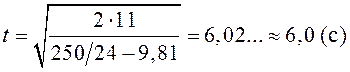Ответ: время подъема груза

2.2.  Прямолинейное движение в горизонтальном направлении

Несмотря на другие условия движения принципиально решение задачи 8 ничем не отличается от решения задачи 7. Отличие состоит лишь в том, что в задаче 8 действующие на тело силы не лежат вдоль одной прямой, поэтому проекции необходимо взять на две оси.

Задача 8. Лошадь везет сани массой 230 кг, действуя на них с силой 250 Н. Какое расстояние пройдут сани, пока достигнут скорости 5,5 м/с, двигаясь из состояния покоя. Коэффициент трения скольжения саней о снег равен 0,1, а оглобли расположены под углом 20° к горизонту.

На сани действуют четыре силы: сила тяги (натяжения), направленная под углом 20° к горизонту; сила тяжести, направленная вертикально вниз (всегда); сила реакции опоры, направленная перпендикулярно опоре от нее, т. е. вертикально вверх (в данной задаче); сила трения скольжения, направленная против движения. Поскольку сани будут двигаться поступательно, все приложенные силы можно параллельно перенести в одну точку – в центр масс движущегося тела (саней). Через эту же точку проведем и оси координат (рис. 8).

На основании второго закона Ньютона запишем уравнение движения:

.                              

Направим ось Ox горизонтально вдоль направления движения (см. рис. 8), а ось Oy – вертикально вверх. Возьмем проекции векторов, входящих в уравнение , на координатные оси, добавим выражение для силы трения скольжения и получим систему уравнений:

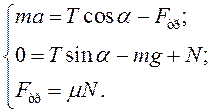
Решим систему уравнений . (Схема решения системы уравнений, подобных системе , обычно одинакова: из второго уравнения выражают силу реакции опоры и подставляют ее в третье уравнение, а затем выражение для силы трения подставляют в первое уравнение.) В результате получим:

.                        

Перегруппируем слагаемые в формуле и разделим ее правую и левую части на массу:

.                        

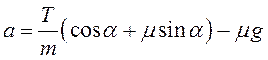Поскольку ускорение не зависит от времени, выберем формулу кинематики равноускоренного движения, содержащую скорость, ускорение и перемещение:

.                                   

Учитывая, что начальная скорость равна нулю, а скалярное произведение одинаково направленных векторов равно произведению их модулей, подставим ускорение и выразим модуль перемещения:

;                     

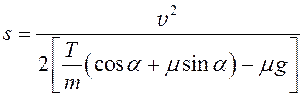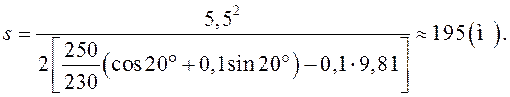
Полученное значение и есть ответ задачи, поскольку при прямолинейном движении пройденный путь и модуль перемещения совпадают.

Ответ: сани пройдут 195 м.

2.3.  Движение по наклонной плоскости

Описание движения небольших тел по наклонной плоскости принципиально не отличается от описания движения тел по вертикали и по горизонтали, поэтому при решении задач на этот вид движения, как и в задачах 7, 8, также необходимо записать уравнение движения и взять проекции векторов на координатные оси. Разбирая решение задачи 9, необходимо обратить внимание на схожесть подхода к описанию различных видов движения и на нюансы, которые отличают решение этого типа задач от решения задач, рассмотренных выше.

Задача 9. Лыжник соскальзывает с длинной ровной заснеженной горки, угол наклона к горизонту которой составляет 30°, а длина равна 140 м. Сколько времени будет длиться спуск, если коэффициент трения скольжения лыж о рыхлый снег равен 0,21?