Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач, страница 3

Ответ: скорость шарика равна  и направлена вертикально вниз; координата равна 8,5 м; перемещение направлено вверх и равно 7,2 м.

1.2.  Равноускоренное движение на плоскости

Условие равноускоренного движения () не требует, чтобы движение происходило вдоль прямой линии. Если при движении тела в прост-ранстве его ускорение (вектор) остается неизменным, то такое движение будет равноускоренным, следовательно, для его описания справедливы все формулы кинематики, полученные для равноускоренного движения. В качестве примера равноускоренного, но не прямолинейного движения, рассмотрим движение тела, брошенного под углом к горизонту.

Задача 2. С края вертикального утеса, возвышающегося над поверхностью моря на 55 м, под углом 60° к горизонту брошен небольшой камень со скоростью . Пренебрегая сопротивлением воздуха, найти, на каком расстоянии от основания утеса камень упадет в воду, и какую скорость при этом он будет иметь.

Решение.

Если пренебречь сопротивлением воздуха, то движение тел вблизи поверхности Земли происходит с постоянным ускорением (), направленным вертикально вниз. Воспользуемся формулами кинематики равноускоренного движения:

;                                    

,                                     

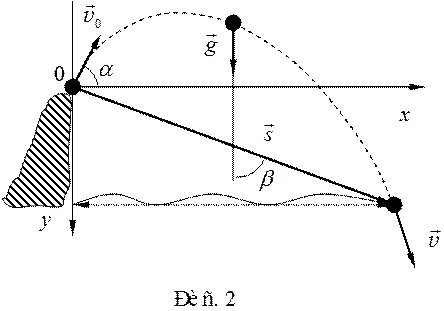но в отличие от предыдущего примера проекции векторов возьмем на две координатные оси, поскольку движение камня происходит не по прямой, а в плоскости. Выберем начало координат в точке бросания камня, ось Ox направим горизонтально от утеса в сторону моря, а ось Oy – вертикально вниз. (Из рис. 2 видно, что при таком выборе системы координат проекции всех векторов, входящих в формулы и , кроме , будут положительны.) Возьмем проекции и получим:

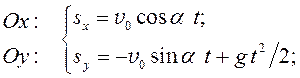
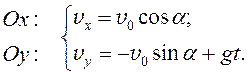
Из рис. 2 видно, что проекция вектора перемещения на ось Oy равна высоте утеса h, а на ось Ox – расстоянию от основания утеса до точки падения камня в воду, которое требуется найти. Определим это расстояние, решая сов-местно систему уравнений . Из второго уравнения системы , решая квадратное уравнение и выбирая положительный корень, выразим время:

.                       

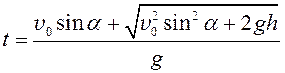Подставляя выражение в первое уравнение системы , получим:

;                

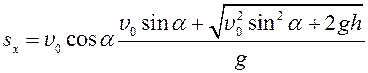Теперь найдем скорость, с которой камень упал в воду. Проекции ско-рости определяются системой , а модуль рассчитывается по формуле:

.            

Подставим в формулу время из выражения и, раскрывая скобки и проведя алгебраические преобразования, получим:

;                                   

.

Этот же результат можно получить иначе. Используя правила векторной алгебры, из выражений и получим:

.                                   

Расписывая скалярное произведение в правой части равенства , получим формулу:

,                              поскольку произведение  есть проекция перемещения на вертикальную ось. Такой же результат можно получить, расписав скалярное произведение еще одним известным способом и подставив проекции векторов  и  на координатные оси (см. начало решения задачи):

,                         

Ответ: камень упадет в воду на расстоянии 37 м от утеса со скоростью 36 .

1.3.  Движение по окружности с постоянной по модулю скоростью

Движение тела по окружности с постоянной по модулю скоростью не является равноускоренным движением, несмотря на то, что модуль ускорения

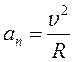                                          остается неизменным, так как вектор ускорения постоянно поворачивается. Ускорение, с которым при этом движется тело, называется центростремительным, или нормальным, так как оно направлено к центру окружности и перпендикулярно вектору скорости.

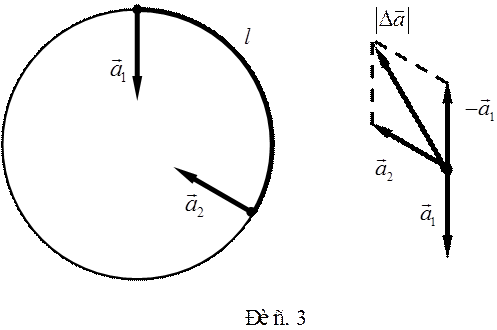
Задача 3. Модель самолета движется с постоянной скоростью по окружности радиусом 6,3 м и пролетает третью часть окружности за 1,2 с. Найти изменение ускорения модели за это время.