Получение плотных отливок. Особенности взаимодействия отливки и формы, страница 15

Для отливок со сложными очертаниями их проекции на плоскость разъема вместо произведения l_oD_o используется площадь проекции отливки на плоскость разъема. При определении силы, действующей на верхнюю полуформу, необходимо учесть силу P_выт, выталкивающую стержни в соответствии с законом Архимеда: Р_выт = ρ_жgV_ст, где V_ст — объем части стержня, погруженного в расплав (без знаковых частей).

Следует отметить два важных обстоятельства относительно силы Р_выт: выталкивающая сила не зависит от глубины погружения, и она изменяется в процессе заливки (погружения) стержня.

Первое обстоятельство является очевидным, так как на какой глубине не находился бы куб (параллелепипед), выталкивающая сила будет одинакова и может быть определена из выражения (рис. 15.4

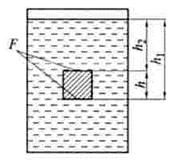
Рис. 15.4. Иллюстрация независимости выталкивающей силы от глубины погружения тела: F— площадь его верхней и нижней поверхности; h₁,h₂ –– расстояния от поверхности жидкости до нижней и верхней поверхностей тела; h — высота тела

Р_выт = ρ_жg(h₁ – h₂)F = ρ_жgV,

где разность высот h₁ – h₂= h — высота куба (параллелепипеда); F— площадь поверхности тела, перпендикулярной чертежу, V — объем куба.

Для иллюстрации второго обстоятельства рассмотрим пять возможных вариантов (рис. 15.5, I — V) и проследим, как изменяется выталкивающая сила по мере погружения (заливки) стержней в зависимости от координаты h (рис. 15.6).

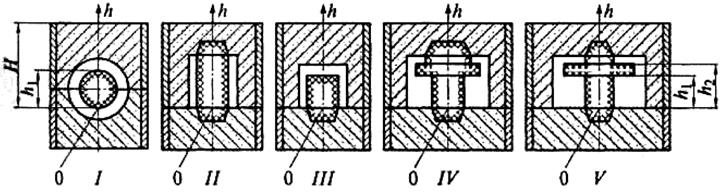
Рис. 15.5. Возможные варианты (I— V) размещения стержней в форме: 0 — начало координат; h — ось ординат; Н, h₁, h₂ — расстояния от начала кoординат

Изменение выталкивающей силы для горизонтального стержня (см. рис. 15.5, I) соответствует классическим представлениям: выталкивающая сила начинает расти от момента соприкосновения стержня с металлом до его полного погружения, затем она остается постоянной, независимой от глубины погружения до окончания заполнения формы (кривая I на рис. 15.6).

362

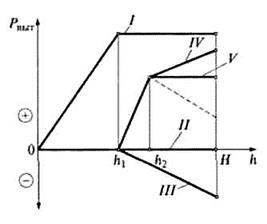
Рис. 15.6. Изменение выталкивающей силы Р_выт при заполнении форм, соответствующих вариантам I—V на рис. 15.5: h, Н, h₁ h₂ — то же, что на рис. 15.5

На схеме II (см. рис. 15.5) выталкивающая сила равна нулю в течение всего времени заполнения, металл называет давление только на боковую поверхность стержня (прямая II на рис 15.6). Для схемы III на рис. 15.5 выталкивающая сила сначала также равна нулю, затем под действием металла на верхнюю поверхность стержня он придавливается силой, возрастающей до окончания заполнения (кривая III на рис. 15.6). Для схемы IV на рис. 15.5 выталкивающая сила равна нулю до высота h₁ затем она начинает расти до h = h₂(кривая IV на рис. 15.6). Дальнейший ход изменения выталкивающей силы будет зависеть от соотношения площадей нижней (F_н) и верхней (F_в) частей стержня по отношению к выступу. При F_в = F_н (см. рис. 15.5, V)выталкивающая сила не будет изменяться и останется постоянной (кривая V на рис. 15.6), при F_в > F_н она будет увеличиваться и этот процесс продолжится до заполнения формы, но с меньшей скоростью, чем в интервале высот h₁...h₂. Наконец, начиная с момента, когда F_в < F_h, выталкивающая сила начнет уменьшаться (штриховая кривая на рис. 15.6) и при h = Н может быть положительной величиной, а может достичь нуля или отрицательных величин (стержень будет придавлен).

В случаях I, II, IV, V нарис. 15.5 имеется горизонтальное сечение стержня, при прохождении которого выталкивающая сила достигает максимума, а затем может уменьшаться. Такое сечение называется «опасным». При решении вопроса о всплытии стержней необходимо помнить об опасном сечении.

15.2. РАСЧЕТ ГРУЗА

Для предотвращения раскрытия стыка формы и ухода металла на верхнюю полуформу, как и в старину, укладывают груз, а также прибегают к различным способам скрепления опок с помощью скоб, болтов, эксцентриковых зажимов и т.п., для выбора которых необходимо знать усилие Р_в.п, действующее на верхнюю полуформу. Собственно, расчет груза G_гри выполняют для определения именно этого усилия, но при этом используют старинное название процедуры «расчет груза».

363