Общая характеристика водного режима и определение стока расчётной обеспеченности реки Томь – г.Междуреченск, страница 29

Вычисляем погрешность среднего многолетнего значения ряда расходов и коэффициент изменчивости.

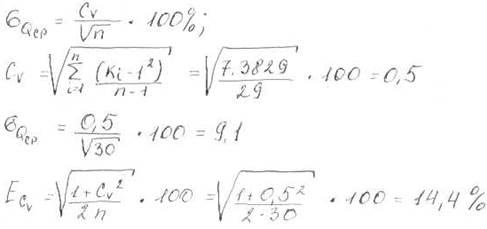
Вычисляем коэффициент асимметрии по приближённой формуле, и его среднеквадратическую погрешность.

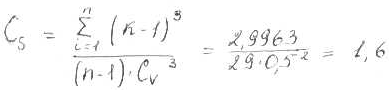
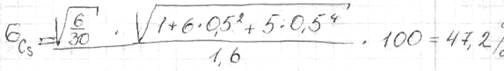
Погрешность вычисления коэффициента асимметрии получили большой, и для выбора расчетной аналитической кривой обеспеченности применяем метод подбора.

Принемаем следующие соотношения:

C_s = 1.5 C_v;   C_{s =} 2C_v;  C_s = 2.5C_v;

Ординаты аналитических кривых определяем по приложению и сводим в таблицу 6.6.

Таблица 6.6.

Ординаты аналитических кривых обеспеченности максимальных многолетних расходов дождевых паводков. р.Томь – г.Междуреченск,   Q_ср.м = 706.2м³/с,  C_v = 0.5

На рисунк 6.4 строим эмпирическую и аналитические кривые обеспеченности максимальных расходов воды дождевого паводка.

По проведённым кривым видно, что наилучшее совпадение, в крайних участков кривой, получено у кривой C_s = 2C_v.

Принимаем коэффициент асимметрии равный 2C_v.

По полученным результатам, заполняем таблицы 6.7 и 6.8.

Таблица 6.7.

Максимальные расходы весенних половодий расчётной реки

Томь - г.Междуреченск.,  Q_ср.п = 1375.4 м³/с. C_v=0.4. C_s=0.87.

Таблица 6.8.

Характеристики максимальных расходов дождевых паводков  расчётной реки Томь - г.Междуреченск., Q_ср.д = 706.2. C_v=0.5. C_s=1.6.

Рассчитываем максимальные расходы весенних половодий и дождевых паводков обеспеченностью 1%, для случая отсутствия наблюдений.

Рассчитываем максимальные расходы воды дождевых паводков на р.Томь – г.Междуреченск, обеспеченностью 1%.

Морфометрические и географические характеристики водосбора:

F = 5880км². L = 169км. I = 5.6%0. f_л = 85%. f_б = 0%. f_оз = 1%.

В виду отсутствия данных наблюдения в расчётном створе, принимаем створ аналог р.Томь – п.Теба. Период наблюдения по аналогу равен двадцать лет, с 1967 – 1996гг.

Лес распределён равномерно по водосбору. В соответствии с таблицами СНиП-2.01.14-83 производим расчёт по редукционной формуле.

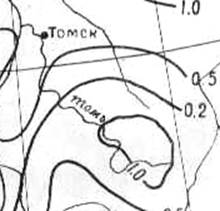
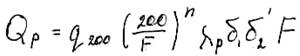
По таблицам находим: n=0.36; c=0,1 (при относительной озёрности, параметр уменьшаем в 2 раза);

Так как лесистость и озёрность одинакова, то в расчётных формулах их не учитываем. Модуль дождевого стока q₂₀₀=1м³/(с*км²),

Определён по карте максимальных модулей дождевого стока рек вероятностью превышения Р=1%.

Максимальный расход воды дождевого паводка вероятностью превышения Р =1% равен:

Q_1%=1*(200/5880)^0.361*5880=1742.9

Сравнивая полученный результат, с результатом полученным по кривой обеспеченности помещённым в таблице 6.6 (Q_1%=1772.6), делаем вывод, что полученные результаты близки по значению.

Рассчитываем максимальный расход весеннего половодья, обеспеченностью 1%.

Морфометрические и географические характеристики водосбора:

F = 5880км². L = 169км. I = 5.6%0. f_л = 85%. f_б = 0%. f_оз = 1%.