Общая характеристика водного режима и определение стока расчётной обеспеченности реки Томь – г.Междуреченск, страница 15

При заполнении табл.3.7., ведём по строчный контроль. В каждой её строке, число в графе 11 равно сумме чисел в графах 7 и 8 и удвоенному значению числа в графе 9. Кроме того, выполняем общий контроль вычислений. Сумма по графам 5 и 6 с учётом знаков равна 0. Сумма графы 11 равна сумме по графам 7,8 и удвоенной по графе 9.

Производим вычисления следующих характеристик:

средние квадратические отклонения

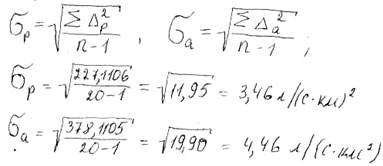
коэффициент корреляции.

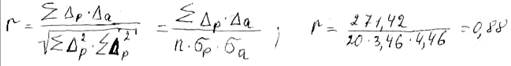
коэффициенты регрессии.

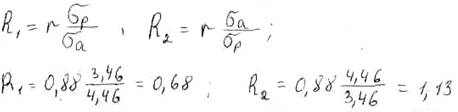
уравнения прямых регрессий расхода Q_p по Q_a   Q_ip – Q_ср.p = R₁(Q_ia – Q_cp.a)

Q_ip = Q_cp.p + R₁(Q_ia – Q_cp.p)

Q_a по Q_p    Q_ia – Q_cp.a = R₂(Q_i.p – Q_cp.a)       

Q_i.a = Q_cp.a + R₂(Q_i.p - Q_cp.a)

Модуля.  M_p    M_a     M_ip = M_cp.p + R₁(M_ia - M_cp.a)

M_a    M_p    M_ia = M_cp.a +  R₂(M_i.p-M_cp.p)

М_1967.р=26.69+0.68(23.22-25.24)=25.32_л/(с.*км²)

Q_1967.p=156.95+0.68(101-109.79)=150.97_м³/с.

М_1977.р=26.69+0.68(23.91-25.24)=25.78_л/(с*км²₎

Q_1977.р=156.96+0.68(104-109.79)=153.01_м³_/с .   и т.д.

Восстановленные значения помещаем в скобках в табл. 3.8.

Вычисляем средние ошибки уравнений регрессии.

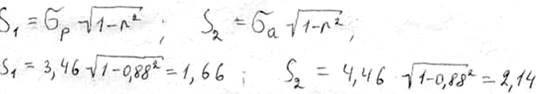
Далее вычисляем: вероятную ошибку коэффициента корреляции.

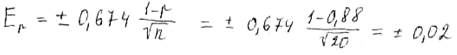
предельную ошибку коэффициента корреляции.

Связь считаем надёжной, так как коэффициент r>0.7

Определяем среднемноголетние значение годового стока расчётной реки, приведённое к длинному ряду. Для этого используем два метода, графический и аналитический.

Графический приём заключается в определении среднемноголетнего значения годового стока расчётной реки по графику связи (рис 3.5). Для этого по среднемноголетнему значению годового стока реки аналога снимаем со средней линии связи соответствующую величину модуля расчётной реки. На построенном графике точки располагаются достаточно  тесно и находятся в квадрантах В и В¹, значит связь прямая. Зависимость считаем удовлетворительной, так как отклонения большей части точек не превышает 15%. По норме стока реки аналога, соответствующие ему значение модуля, по расчётному свору определяем графически. По полученной графической зависимости, восстанавливаем все годовые значения стока расчётного створа. Полученные данные заносим в таблицу (3.8).

Таблица 3.8

Восстановленные значения стока расчётной реки графическим методом.

Р.Томь – г.Междуреченск.

А затем получаем их средние значения М_ср.= 26.99л/(с*км²). Такой приём при очень большом количестве определений может провести к увеличению ошибок. При этом способе приведения среднего многолетнего значения модуля (или расхода) коэффициент изменчивости стока C_{v в расчётном створе вычисляем по формуле:}

           C_v=A*M_cp.a/M_cp.p*C_v.a

            _{L =} 38⁰   A=tg_L=0.78    M_cp._р=26.99л/(с*км²)

С_v=0.78*25.24/26.69*0.17=0.13