Другие предметы \ Гидрологические расчеты

Общая характеристика водного режима и определение стока расчётной обеспеченности реки Томь – г.Междуреченск, страница 28

Вычисляем погрешность среднего многолетнего значения ряда расходов и коэффициент изменчивости.

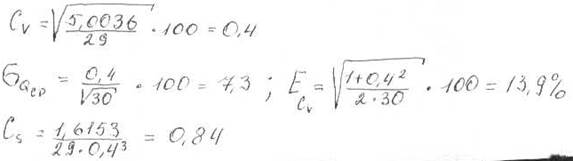
Погрешность вычисления коэффициента асимметрии получили большой, и для выбора расчетной аналитической кривой обеспеченности применяем метод подбора.

Принемаем следующие соотношения:

Cs = 1.5 Cv;   Cs = 2Cv;  Cs = 2.5Cv;

Ординаты аналитических кривых определяем по приложению и сводим в таблицу 6.4.

Таблица 6.4.

Ординаты аналитических кривых обеспеченности максимальных многолетних расходов весеннего половодья. р.Томь – г.Междуреченск,   Qср.м = 1375.4 м3/с, Сv = 0.4

Cs

P%

1

10

50

95

1.5Cv

kp

2.11

1.54

0.956

0.415

Qp

2902.1

2118

1314.9

570.8

2Cv

Kp

2.17

1.54

0.944

0.454

Qp

2984.6

2118

1298.4

624.4

2.5Cv

Kp

2.23

1.53

0.935

0.475

Qp

3067

2104.3

1286

653.3

На рисунке 6.3 строим эмпирическую и аналитические кривые обеспеченности максимальных расходов воды весеннего половодья.

По проведённым кривым видно, что наилучшее совпадение, особенно в крайних участков кривой, получено у кривой Cs = 2Cv.

Принимаем коэффициент асимметрии равный 2Cv.

Подобным методом вычисляем кривую обеспеченности максимальных расходов воды дождевых паводков в таблице 6.5.

Таблица 6.5.

Вычисление методом моментов по удлиненному ряду дождевых паводков     кривой обеспеченности максимальных расходов воды р.Томь – г.Междуреченск, за 1967 – 1996гг.

№

п/п

Год

Qi

М3/с

Qуб

М3/с

K=Qуб/Qср

k-1

(k-1)2

(К-1)3

P=(m/n+1)*100

1

1967

(535

1500

2.1241

1.12

1.2633

1.4199

3.23

2

1968

(1300

1465

2.0744

1.07

1.1543

1.2402

6.45

3

1969

(691

1300

1.8408

0.84

0.7069

0.5943

9.68

4

1970

(744

1263

1.7884

0.79

0.6215

0.4900

12.9

5

1971

(573

1243

1.7600

0.76

0.5776

0.4390

16.13

6

1972

(803

1064

1.5066

0.51

0.2566

0.1300

19.35

7

1973

(1064

897

1.2701

0.27

0.0730

0.0200

22.58

8

1974

(471

878

1.2432

0.24

0.0592

0.0144

25.81

9

1975

(758

803

1.1370

0.14

0.0188

0.0026

29.03

10

1976

(629

758

1.0733

0.07

0.0054

0.0004

32.26

11

1977

245

744

1.0535

0.05

0.0029

0.0002

35.48

12

1978

1500

700

0.9912

-0.01

0.0001

0.0000

38.71

13

1979

414

696

0.9855

-0.01

0.0002

0.0000

41.94

14

1980

696

691

0.9784

-0.02

0.0005

0.0000

45.16

15

1981

476

648

0.9175

-0.08

0.0066

-0.0006

48.39

16

1982

648

629

0.8906

-0.11

0.0120

-0.0013

51.61

17

1983

452

620

0.8779

-0.12

0.0149

-0.0018

54.84

18

1984

620

573

0.8113

-0.19

0.0356

-0.0067

58.06

19

1985

250

535

0.7575

-0.24

0.0588

-0.0143

61.99

20

1986

1263

476

0.6740

-0.33

0.1063

-0.0346

64.51

21

1987

420

471

0.6669

-0.33

0.1109

-0.0370

67.74

22

1988

1465

452

0.6400

-0.36

0.1296

-0.0467

70.97

23

1989

432

432

0.6117

-0.39

0.1508

-0.0585

74.9

24

1990

700

420

0.5947

-0.41

0.1643

-0.0666

77.42

25

1991

878

420

0.5947

-0.40

0.1643

-0.0666

80.64

26

1992

246

414

0.5843

-0.41

0.1712

-0.0709

83.87

27

1993

1243

354

0.5013

-0.50

0.2488

-0.1241

87.10

28

1994

354

250

0.3540

-0.65

0.4173

-0.2696

90.32

29

1995

897

246

0.3483

-0.65

0.4247

-0.2768

93.55

30

1996

420

245

0.3469

-0.65

0.4265

-0.2786

96.77

cумма

21187

21187

30.00

0.00

7.3829

2.9963

Ср.     Средние

706.2

706.2
Скачать файл