Использование понятия ударного коэффициента позволяет и в этом случае внести существенные упрощения в расчёт токов короткого замыкания в более сложных цепях: вместо решения соответствующих дифференциальных уравнений (особенно синхронных машин) расчёт можно свести к чисто алгебраическим операциям – определению периодической составляющей тока через э.д.с. Еm и сопротивление короткого замыкания zk или xk с последующим применением Ку.
Для проверки элементов схем электроснабжения на термическую стойкость и проверки выключателей по отключающей способности необходимо знать действующие значения токов короткого замыкания.
Прежде всего оговорим условность принятой терминологии. Она заключается в том, что называя действующее значение, например, тока в произвольный момент переходного процесса, будем иметь в виду, что оно определяется как среднеквадратичное значение за один период Т, в середине которого находится рассматриваемый момент времени. В соответствии с этим при известной зависимости i = f(t) для действующего значения тока в момент t можно записать:
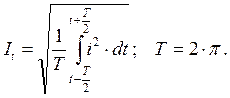
Зависимость i = f(t) в общем случае очень сложна. Поэтому для упрощения подсчета It принимают, что за рассматриваемый период обе слагающие тока не изменяются, т. е. амплитуда периодической слагающей и апериодическая слагающая неизменны; каждая из них равна своему значению в данный момент t. Такое допущение относительно периодической слагающей делают, когда источником является генератор конечной мощности; для условий же § 3-2 постоянство амплитуды соблюдается.
Сказанное иллюстрирует рис. 3-5, где для общности принято, что амплитуда периодической слагающей тока изменяется. Для заданного момента t амплитуду этой слагающей определяют по соответствующей огибающей (см. пунктирные линии); при этом действующее значение рассматриваемой слагающей в этот момент находят как
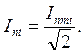
![]()
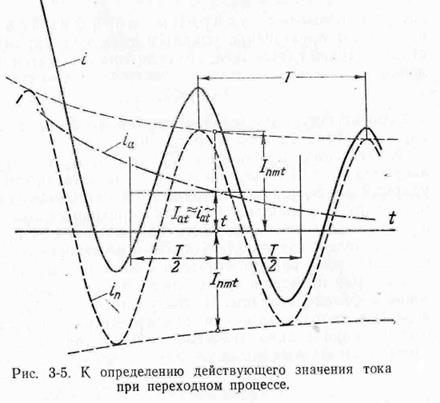
Соответственно действующее значение апериодической слагающей за один период при принятом допущении равно ее мгновенному значению в момент, находящийся посредине данного периода (рис. 3-5), т. е.
Iat = iat
Действующее значение полного тока в тот же момент будет:
![]()
т. е. оно определяется знакомым выражением для действующего значения несинусоидального тока.. Точность определения по (3-11) вполне удовлетворяет требованиям практики.
Наибольшее действующее значение полного тока короткого замыкания /у имеет место за первый период переходного процесса. При условии, когда iа/о/ =I nm, его можно определить по (3-11), придав последнему следующий вид:
![]()
где kу – ударный коэффициент.
Определим теперь, какое максимальное действующее значение полного тока может возникнуть в короткозамкнутой цепи за первый период переходного процесса после возникновения короткого замыкания:
Предположив, что амплитуда фазного тока в момент короткого замыкания равна Iпm, с учётом того, что
Прописными буквами будем обозначать мгновенные значения токов, строчными – действующие.
Предположив, что амплитуда периодической составляющей фазного тока в момент короткого замыкания равна Iпm, с учётом того, что:
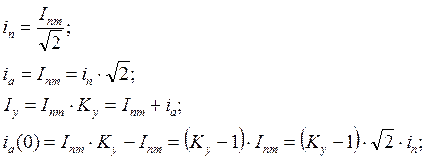
получим:
![]()
Поскольку известно, что величина Ку лежит в диапазоне
1 ≤ Ку ≤ 2,
отношение величины термического тока за первый период к действующему значению периодического тока будет лежать в диапазоне
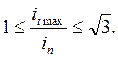
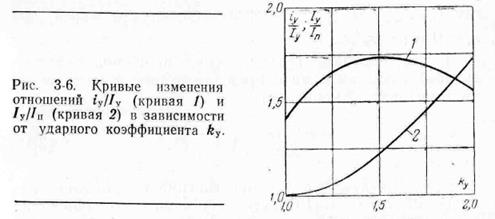
На рис. 3.6 показаны кривые изменения отношений Iy/IП и iy/Iy в функции ky. Как видно, отношение iy/Iy изменяется в сравнительно узких пределах и его
максимум (![]() ) наступает при ky.
) наступает при ky.
Лекция 3
Практические методы расчета токов КЗ
в разветвленной цепи
Как следует из предыдущей лекции, основной величиной, подлежащей определению, является значение периодической составляющей тока короткого замыкания I'' в разветвлённой цепи. Зная её, легко определить ударный ток и действующее значение тока в любой момент времени. Расчёт Iп не вызывает больших трудностей. Достаточно определить результирующее сопротивление от каждого источника ЭДС до точки короткого замыкания, тогда, зная величины ЭДС, токи от каждой из них в точку короткого замыкания можно определить по формуле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.