Электротехника \ Переходные процессы в системах электроснабжения

Электромагнитные процессы при сохранении симметрии трёхфазной цепи. Введение и переходные процессы в простых цепях при коротком замыкании, страница 2

     Простейшая трёхфазная цепь – это симметричная трёхфазная цепь с сосредоточенными параметрами при отсутствии в ней трансформаторных связей (рис.2.1).    


Рис. 2.1  Простейшая трёхфазная цепь

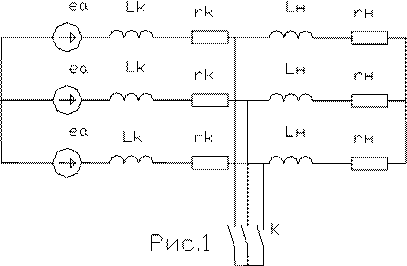Рассмотрим электромагнитный переходный процесс в такой цепи при замыкании выключателя К при условии, что её питание осуществляется от источника, собственное внутреннее сопротивление которого равно нулю и его напряжение, изменяясь с постоянной частотой, имеет неизменную амплитуду1. Обычно такой источник называют источником бесконечной мощности.

Включение его в схему, вообще говоря, соответствует теоретическому пределу, когда изменение внешних условий не влияет на работу самого источника. Практически это имеет место, например, при коротких замыканиях в относительно маломощных электрических установках или протяжённых сетях, питаемых от крупных энергетических систем. В системах электроснабжения промышленных предприятий это условие, как правило, выполняется.

С исследованием переходных процессов в подобных условиях студенты должны быть знакомы из курса теоретических основ электротехники. Поэтому задачей данного курса является кратко напомнить основные выводы и положения такого исследования, отметить особенности многофазной цепи по сравнению с однофазной, привести некоторые упрощённые методы расчёта и обратить внимание на влияние ряда факторов.

Короткое замыкание в заданный момент времени t0осуществляется контактором К, за которым установлена закоротка, что равносильно возникновению металлического трёхфазного короткого замыкания в точке, лежащей между двумя участками данной цепи.

Запишем выражения, определяющие доаварийный установившийся режим работы цепи. Очевидно, что в силу её симметрии достаточно рассматривать процессы только в одной фазе. Этим приёмом мы будем очень часто пользоваться в дальнейшем.

          iA=Inm0 cos(ωt-φ),                                                (2.1)



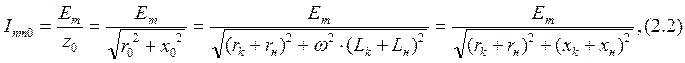где Inm0 – амплитуда периодической составляющей тока

       установившегося режима;

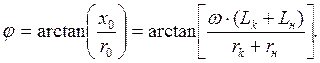
Процессы после возникновения короткого замыкания

Задано начальное условие: при t=t0, ia(t0)=ia0. В этот момент происходит короткое замыкание.

¨  Токи в нагрузке

Короткое замыкание как бы «отсекает» нагрузку от источника питания. Напряжение в точке короткого замыкания становится равным нулю. Токи в ней описываются уравнениями вида

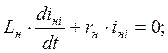 (i = A,B,C)                            (2.3)

Учитывая начальные условия, решение для каждой фазы получим в виде:

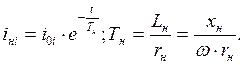                                        (2.4)

Процессы, подчиняющиеся законам изменения вида

 и 

называются экспоненциальными, потому что переменные x и y изменяются по закону экспоненты. Это значит, что за каждый отрезок времени t = Т переменная х уменьшается на 63,2% от значения в начале этого интервала, а переменная y увеличивается на 63,2% от разности между установившимся значением и значением в начале интервала, то есть:

t

Δх

х

Δ y

y

0

(0-1)•0,632 А=-0,632 А

A

(1-0) •0,632 А=0,632 А

0

T

(0-0,368)•0,632 А=-0,233 А

0,368 A

(1-0,632) •0,632 А=0,233 А

0,632 А

2T

(0-0,135)•0,632 А =-0,085 A

0,135 A

(1-0,865)•0,632 А=0,085 А

0,865 А

3T

—

0,050 A

—

0,95 А


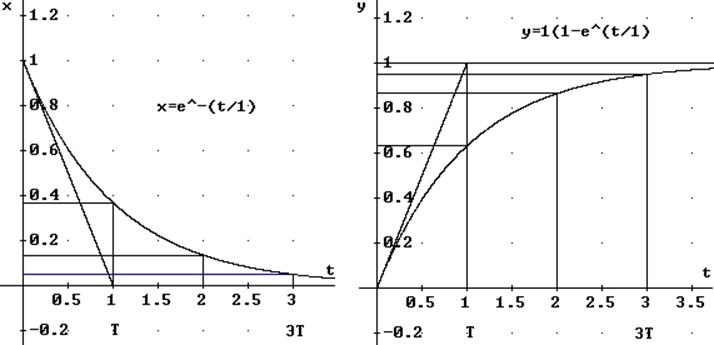          Рис. 2.2 Ход протекания во времени экспоненциальных процессов

             при А = 1; Т = 1 с

Для процессов, подчиняющихся экспоненциальному закону, принято считать, что они полностью затухают за время, приблизительно равное трём постоянным времени. t = 3Т. В более точных расчётах считают, что за это время переменная затухает до 5% или нарастает до 95% от исходной величины.

Из графиков, приведённых на рис. 2.2, видно, что величину постоянной времени Т можно определить двумя способами:

Скачать файл