Электромагнитные процессы при сохранении симметрии трёхфазной цепи. Введение и переходные процессы в простых цепях при коротком замыкании, страница 11

Кроме того, мы будем рассматривать идеализированную машину, приняв ряд основных допущений:

          Уравнения, описывающие работу  и переходные процессы СМ можно значительно упростить, если использовать специальную систему координат (0,d,q), оси которой строго совмещены с продольным и поперечным направлениями вращающегося ротора машины.

1  Отсутствует насыщение магнитопроводов (это наиболее сильное и далёкое от истины допущение). Однако оно позволяет использовать метод наложения процессов и, как следствие этого, использовать теорию двух реакций (по продольной и поперечной осям машины), являющейся основой для записи уравнений.

2  Распределение кривых индукции магнитного поля в воздушном зазоре синусоидально.

3  Обмотки ротора и его магнитная система симметричны относительно осей q и d. Обмотка статора симметрична относительно осей a, d, c.

4  Существуют единый для всех эквивалентных контуров СМ магнитный поток взаимной индукции и независимые от него и друг друга потоки рассеяния каждого из контуров.

          Тогда СМ машину можно изобразить так, как это показано на рис. 5.1.

          Рис. 5.1. Принципиальная схема СМ

          Ротор вращается против часовой стрелки с угловой частотой ω. Магнитное поле, образованное трёхфазной системой токов, протекающих в неподвижных контурах статора (рис.5.2) также вращается в воздушном зазоре с той же частотой ω (в установившихся режимах ω = ω_с = 314,159 рад/с).

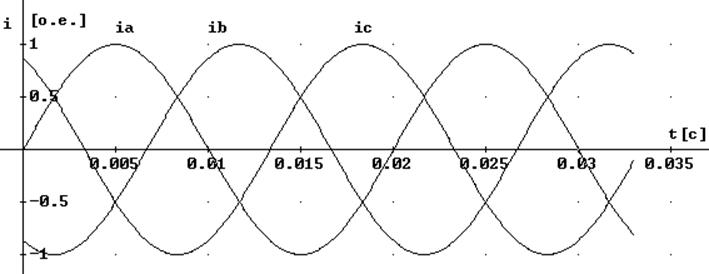
          Рис. 5.2. Трёхфазная система статорных токов

Ротор и вращающееся поле статора в установившемся режиме работы СМ неподвижны друг относительно друга, т.е. вращаются синхронно. Это и  дало возможность определить данный класс электрических машин как синхронные машины. Это эе обстоятельство сделало весьма эффективным использование совмещённой с ротором, т.е. вращающееся с синхронной скоростью координатной системы d-q. Наблюдатель, условно помещённый на ротор, в установившемся режиме СМ машины будет воспринимать все переменные, характеризующие процессы в статоре, как постоянные величины.

          Использование координатной системы q-d предполагает замену трёх физических контуров статора СМ (a, b, c) двумя эквивалентными (q, d). Контуры d и q  вращаются вместе с координатной системой q-d, поэтому параметры СМ, оцениваемые в координатной системе q-d, есть величины постоянные, и токи I_q и I_d в установившихся режимах работы постоянны.

Переход от координатной системы аbc

к координатной системе 0qd

          На рис.5.3 приведена неподвижная система координат abc. Изображающий вектор тока I вращается против часовой стрелки и его проекции на оси фаз образуют систему фазных токов i_a, i_b, i_c. Положение изображающего вектора определяется углом τ, который отсчитывается от направления оси фазы a. Координатная система q-d вращается в том же направлении. Её положение определяется углом γ. Очевидно, что

i = │I│;

i_q = i cos(τ – γ);

i_d = i sin(τ – γ);

Введём переменную ρ = 2 π/3, тогда соотношение между проекциями изображающего вектора тока на оси q,d и фазными токами можно записать в виде:

          i_a  = i₀ + i_q cosγ – i_d sinγ, (из векторной диаграммы на рис.5.2)

по аналогии:

          i_b = i₀ + i_q cos(γ – ρ) – i_d sin(γ – ρ),                                               (5.1)

          i_c = i₀ + i_q cos(γ + ρ) – i_d sin(γ + ρ);

Этот переход, а также обратный переход от осей 0qd к осям abc можно записать изящнее, используя матрицы преобразований:

             1      cosγ             -sinγ

S_qa =     1     cos(γ – ρ)     -sin(γ – ρ)         - преобразование Блонделя  (5.2)

             1     cos(γ + ρ)     -sin(γ + ρ)

               1/3               1/3                          1/3

C_aq =   2/3*cosγ     2/3*cos(γ – ρ)       2/3*сos(γ + ρ)                     (5.3)

           2/3*sinγ     2/3*sin(γ – ρ)         2/3*sin(γ + ρ)

I_abc =  S_qa I_0qd;                                     (5.4)