Электромагнитные процессы при сохранении симметрии трёхфазной цепи. Введение и переходные процессы в простых цепях при коротком замыкании, страница 3

-  Провести касательную к кривой из точки начала переходного процесса. Точка её пересечения с нулевой линией (или установившимся значением переменной) даст величину постоянной времени.

-  Определить время достижения переменной величины 5% от начального (или 95% от установившегося) значения переменной. Разделив это время на 3, получим значение постоянной времени.

§  Токи в нагрузке (справа от точки короткого замыыкания)

В нашем случае ток в каждой фазе нагрузки экспоненциально затухает от значения i_oi, которое он имел в момент возникновения короткого замыкания, до нуля с постоянной времени Т_н.

          Величина каждого фазного тока в момент возникновения короткого замыкания зависит от фазы э.д.с. Y. В разных фазах она будет разная, но всегда будет соблюдаться условие

i_A0 + i_B0 + i_C0 = 0.

Если предположить, что угол между осью вещественных и вектором э.д.с. е_А Y_A=0, то в этот момент токи и напряжения будут расположены, как показано на векторной диаграмме а) на рис. 2.3. При Y_А=p/2 – как на диаграмме б).

Рис. 2.3 Изображающие векторы трёхфазных переменных

              а) Ψ_а = 0; φ ≈ π/2;    i_A = 0; i_B = -√3 I_{пер m0}; i_C = √3 I_{пер m0};

              б) Ψ_а = π/2; φ ≈ π/2; i_A = I_{пер m0}; i_B = i_C = -0,5 I_{пер m0};

Видно, что ток в фазе нагрузки будет максимальным при прохождении э.д.с. этой фазы через нуль, т.е. при Y=p/2. Токи в двух других фазах при этом будут равны между собой и составлять по модулю половину первого тока. Процесс затухания токов в нагрузке будет протекать примерно так, как показано на рисунке 2.4.

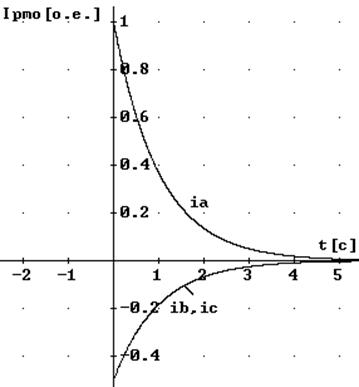
Рис. 2.4 Протекание токов в фазах

              нагрузки после  короткого

              замыкания

¨  Токи в короткозамкнутой части цепи

Решение дифференциального уравнения, вытекающего из уравнения Кирхгофа для каждой из фаз:

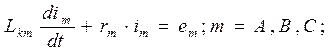                                                                                               (2.5)

содержит две составляющие:

где i_{m пер.} – вынужденная периодическая составляющая фазного тока, обя-

       занная своим существованием наличию питающей фазной э.д.с.

      i_{m апер.} – свободная апериодическая составляющая; она возникает в соот-

       ветствии с принципом постоянства потокосцепления и уравнове-

       шивает мгновенно возникающий скачок периодической составля-

       ющей таким образом, чтобы в первый момент короткого замыка-

       ния ток фазы равнялся току до короткого замыкания.

Далее выкладки будем производить только для фазы А:*

 ψ – угол, характеризующий фазу э.д.с.  е_а в момент короткого замыкания.

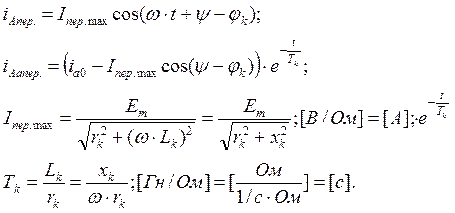       Он может лежать в диапазоне 0≤ψ≤π/2.

Рассмотрим оба варианта, выберем для последующих расчётов наиболее тяжёлый и наиболее лёгкий из них, а остальные будут промежуточными случаями.

          Снова рассмотрим два варианта начальной фазы ЭДС при коротком замыкании:

1.  Ψ=π/2; t=0; φ_k≈π/2; (самый тяжёлый случай)

В первый момент времени после возникновения короткого замыкания:

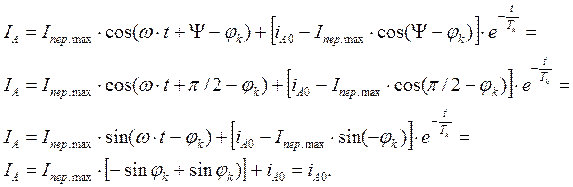
То есть ток в первый момент после короткого замыкания равен току в последний момент до короткого замыкания

Периодическая составляющая тока короткого замыкания фазы А

Апериодическая составляющая:

          Таким образом, в момент возникновения короткого замыкания ток в фазе «А» в этом расчётном случае равен:

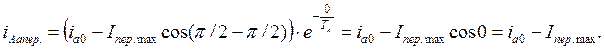i_А│t=t0 =  i_{А пер.│t=t0}+ i_{А апер.│t=t0} = I_{пер. max}+i_А0 - I_{пер. max} = i_a0,

то есть току в этой фазе до возникновения короткого замыкания, а его периодическая и апериодическая составляющие максимальны. Вектор апериодической составляющей тем больше, чем меньше ток фазы А в момент короткого замыкания. В пределе (при бесконечном сопротивлении нагрузки) начальное значение апериодической составляющей по величине равно амплитуде периодической составляющей и противоположно начальному значению периодической составляющей по знаку.