Электромагнитные процессы при сохранении симметрии трёхфазной цепи. Введение и переходные процессы в простых цепях при коротком замыкании, страница 14

          В результате уравнение контура возбуждения можно получить в виде

                                                  (5.1 )

где 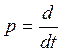 - условная запись математическая запись оператора дифференцирования по реальному времени, введённая для сокращения записи.

          Иногда более удобно пользоваться уравнением контура возбуждения, записанным относительно переходной ЭДС E^'_q:

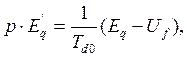                                                                      (5.1 )

где E_q – ЭДС статора за синхронной реактивностью, U_f – относительное значение напряжения, приложенного к зажимам контура возбуждения.

          Поскольку постоянная времени T_do = 5 ÷ 12 с весьма велика, производная  обычно очень мала, поэтому в некоторых задачах можно говорить, что E^'_q = cons. Это допущение во многих случаях допустимо и упрощает решение.

          Запись выражений для потокосцеплений контуров с использованием синхронных и переходных ЭДС характерен  для системы относительных единиц, введённой А.А.Горевым.

          Таким образом, система уравнений синхронной машины, работающей на систему бесконечной мощности (рис.6) при принятых допущениях:

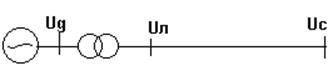
Рис.5

§  не учитываются переходные процессы в статоре;

§  не учитываются трансформаторная э.д.с. и э.д.с. скольжения;

§  не учитываются демпферные контуры

имеет следующий вид:

Уравнения статорной цепи

     Относительно U_Г                                                                       Относительно U_С

                            

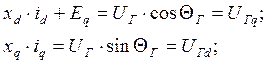
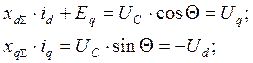
Активная мощность турбогенератора (x_d = x_q):

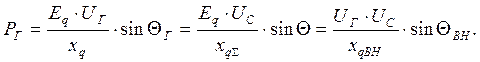
При принятых допущениях все уравнения статорной цепи алгебраические.

Уравнения цепи возбуждения

                           

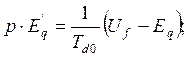
Уравнение движения ротора

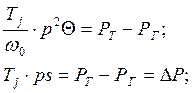
где оператор 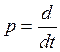означает операцию дифференцирования по времени.

          Таким образом, при постоянстве скорости синхронная машина описывается дифференциальным уравнением третьего порядка, а при учёте изменения скорости вращения ω, скольжения s и фазового угла Θ – систему дифференциальных уравнений третьего порядка.

          В установившемся режиме (р=0)

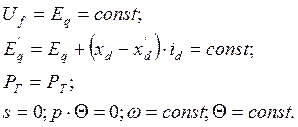
Процесс начального возбуждения

          Синхронная машина вращается с постоянной номинальной скоростью, статорная цепь разомкнута, ток генератора равен нулю. На обмотку возбуждения скачком подаётся напряжение возбуждения холостого хода U_f = 1.

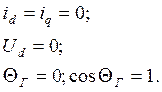
          С учётом этого из статорных уравнений получим:

Из уравнения ротора

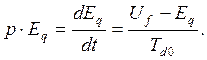
Решение этого уравнения позволяет получить решение для напряжения генератора U_Г в системе координат q-d имеет вид:

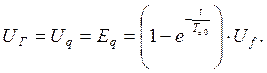
          Для перехода в систему фазных координат a-b-c следует применить полученную ранее матрицу C_qa:

.

В результате, с учётом того, что угол γ = ω₀t, поучим:

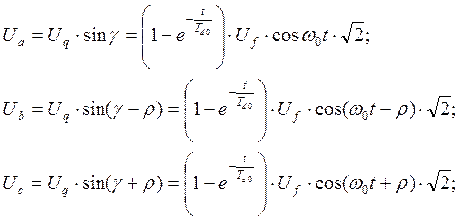
Трёхфазное короткое замыкание синхронной машины

в режиме холостого хода

При внезапном трёхполюсном коротком замыкании синхронной машины возникает электромагнитный переходный процесс, характеризующийся быстрым возрастанием и последующим затуханием до установившихся значений токов статорных и роторных контуров. Математический анализ  его протекания  сводится к решению системы линейных дифференциальных уравнений.

Обычно принимаются следующие допущения:

1.  Синхронная машина не имеет демпферных контуров.

2.  Скольжение s = 0 (механическая постоянная времени настолько велика, что скольжение в течение переходного процесса короткого замыкания не изменяется).

3.  Исходный режим работы – холостой ход.

4.  Регулирование возбуждения в процессе короткого замыкания отсутствует, т.е. U_f = E_r= const.

В этом сучае переходные процессы в синхронной машине описываются системой дифференциальных уравнений в системе относительных единиц А.А.Горева.

Составляющие решения этой системы можно получить в форме:

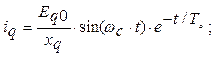
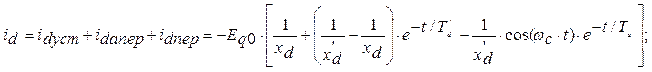
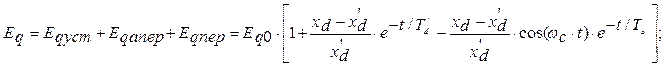       (2)

где:

E_q0[о.е.] – э.д.с. за синхронной реактивностью (ток возбуждения   в исходном  режиме до начала короткого замыкания;