Методология логистики. Модели перерабатывающего элемента. Модели накопительного элемента, страница 17

.

(5.51)

Уровень запаса на складе перед его пополнением  определяется как уровень запаса после  пополнения склада  за вычетом месячного спроса С_n (табл. 5.2)

(5.52)

Наконец уровень запаса на складе в точке заказа  определится как сумма величины запаса на складе перед его пополнением  с учетом расхода продукции в течение времени выполнения заказа

.

Необходимо заметить, что во всех приведенных формулах параметр n означает номер итерации, то есть номер заказа.

Результаты расчетов представим в табличной форме (табл. 5.3). Последовательность расчетов следующая: в первую очередь заполняются столбцы "точки заказа" и "точки пополнения запасов", значение которых увеличивается на время цикла (20 дней); расчет остальных параметров для первой строки (первого заказа n=1) отличается от расчетов для следующих заказов. Так величина  равна сумме рассчитанного размера оптимального заказа и заданного резервного запаса B; далее рассчитывается значение столбца "уровень запасов перед пополнением"  по формуле (5.51); затем определяется "точка заказа"  по формуле (5.52); в последнюю очередь рассчитывается значение "объем заказа"  по формуле (5.50). Например, для первой строки =q₀ + B =170 + 150 = 320 ваг.;  = 320 - 60 = 260 ваг.;  = 260 + 3 × 5 = 275 ваг.;  = 320 - (275 - 8,5 × 5)=87,5 ваг. Для второй строки (второй итерации n=2) =+=87,5 + 260=347,5 ваг.; =347,5 -80=267,5 ваг.; =267,5+4×5 = 287,5 ваг.; =347,5 - (287,5 - 8,5 × 5) = 102,5 ваг. и т.д.

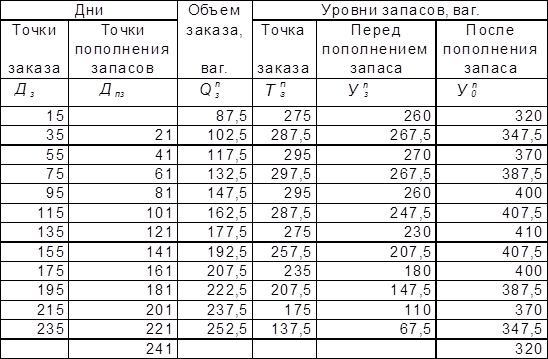
Таблица 5.3

Динамика изменения запасов в системе с фиксированным интервалом между поставками и переменным спросом

Представленные расчеты удобно выполнять при помощи электронных таблиц. В качестве примера приведем фрагмент электронной таблицы в формате Excel, при помощи которой была заполнена табл. 5.3.

Из табл. 5.3 видим, что минимальный уровень запаса  колеблется от 67,5 до 267,5, причем с увеличением спроса величина минимального запаса снижается. В системе с регулярным и надежным интервалом между поставками минимальный запас на складе в момент поступления новой партии в принципе может быть равен нулю. Поэтому в данной системе гарантированный запас можно снизить на 67,5 вагонов до 150-67,5=92,5 вагонов. При этом годовые затраты на хранение продукции на складе также снижаются.

Таблица 5.4

Таблица Excel для расчета динамики запасов

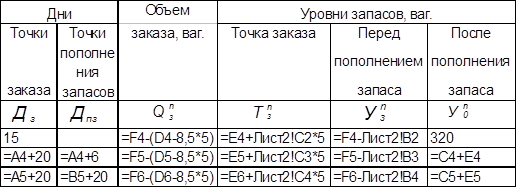В табл. 5.4 имеется ссылка на второй лист электронной таблицы (Лист2). Он содержит данные об изменении спроса на поставку продукции (табл. 5.2).

В данном примере рассмотрен идеальный случай, когда спрос на продукцию растет равномерно. Очевидно, что на практике размер спроса — величина случайная, подчиняющаяся определенному закону распределения. Выполнив необходимые статистические расчеты и получив характеристики этого закона распределения, можно выполнить процедуру генерации случайной величины, т.е. прогнозировать колебания спроса (описание соответствующей методики приводится в [17]).Полученные размеры спроса подставляются в табл. 5.2 (Лист2 электронной таблицы) и в результате получаем размер минимального запаса на складе. Варьируя величиной резервного запаса, добиваются отсутствия отрицательных значений величины минимального запаса на складе.

Еще более интересные результаты можно получить, построив имитационную модель системы управления запасами. С ее помощью появляется возможность проводить более сложные эксперименты с целью определения не только рационального уровня резервного запаса, но и выбора оптимальной тактики заказа ресурсов таким образом, чтобы склад не стал местом концентрации запасов, но и не возникали необоснованно большие издержки из-за отсутствия продукции.